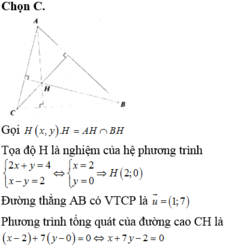
Bài 3.12: Tam giác ABC biết AB x y : 5 2 6 0 và AC x y : 4 7 21 0 và H(0;0) là trực tâm của tam giác. Tìm tọa độ điểm A B

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC có đỉnh B(-6;4), phương trình cạnh AC: x-y-2=0, đường cao AH: 7x-y+4=0. Tìm ptr hai cạnh còn lại
Bài 2: Cho tam giác ABC. Gọi E, F, K là trung điểm các cạnh AB, AC, BC. Cho biết ptr EF: x-y+3=0, FK: 3x+2y-6=0. Viết ptr ba cạnh của tam giác.
help me
1.
A có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x-y-2=0\\7x-y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-3\end{matrix}\right.\Rightarrow A=\left(-1;-3\right)\)
Phương trình đường thẳng AB: \(\dfrac{x+1}{-5}=\dfrac{y+3}{7}\Leftrightarrow7x-5y+22=0\)
Đường thẳng BC đi qua B và vuông góc với AH có phương trình: \(x+7y-22=0\)
Đúng 1
Bình luận (0)
1. Trong mặt phẳng Oxy cho tam giác ABC có trọng tâm G(−2; 0) biết phương trình các cạnh AB, AC theo thứ tự là 4x+y+14=0; 2x+5y-2=0. Tìm tọa độ các đỉnh A, B, C.
2.Lập phương trình các cạnh AB, AC của tam giác ABC biết đường tuyến CM có phương trình 2x+y-6=0, A(1; 1) và cạnh BC có phương trình x+y-6=0
Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là: AB: 7x – y+ 4 0 và BH: 2x+ y- 4 0; AH: x - y -2 0 Phương trình đường cao CH của tam giác ABC là: A. 7x- y+ 2 0 B. 7x+y-2 0 C. x+ 7y + 2 0 D. x+ 7y-2 0
Đọc tiếp
Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là:
AB: 7x – y+ 4= 0 và BH: 2x+ y- 4= 0; AH: x - y -2= 0
Phương trình đường cao CH của tam giác ABC là:
A. 7x- y+ 2= 0
B. 7x+y-2= 0
C. x+ 7y + 2= 0
D. x+ 7y-2= 0
Hai đường thẳng AH và BH cắt nhau tại H nên tọa đô của H là nghiệm hệ
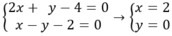
Vậy H( 2; 0)
Do CH vuông góc với AB mà AB: 7x – y + 4= 0 nên CH có
![]()
Suy ra; phương trình CH:
1(x-2) + 7( y-0) = 0
Hay x+ 7y -2= 0
Chọn D.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho
a.tam giác ABC biết A( 3 ;- 4) và các đường cao kẻ từ B và C lần lượt có phương trình 7x - 2y - 1 = 0 và 2 x - 7 y - 6 = 0. Lập phương trình 3 cạnh của tam giác ABC
b. Cho hình chữ nhật ABCD có phương trình AB: x - 2 y - 1 = 0 và BD: x - 7 Y + 14 = 0 .tìm tọa độ các đỉnh của hình chữ nhật biết AC đi qua điểm M( 2; - 1)
Xem chi tiết
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là AB: 7x-y+40; BH2x+y-40; AH: x-y-20. Phương trình đường cao CH của tam giác ABC là A. 7x-y0 B. x-7y-20 C. x+7y-20 D. 7x+y-20
Đọc tiếp
Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là AB: 7x-y+4=0; BH=2x+y-4=0; AH: x-y-2=0. Phương trình đường cao CH của tam giác ABC là
A. 7x-y=0
B. x-7y-2=0
C. x+7y-2=0
D. 7x+y-2=0
Cho tam giác ABC có AB: 2x- y + 4= 0; AC: x- 2y -6= 0; điểm B và C cùng thuộc Ox. Phương trình phân giác ngoài của góc BAC là:
A. 3x- 3y -2= 0
B.x+ y+10= 0
C.2x+3y+2= 0
D.x+ y-1= 0
Đáp án A
Do B ; C cùng thuộc Ox nên suy ra B( -2 ; 0) và C( 6 ; 0)
Gọi M( x ; y) thuộc đường phân giác của góc BAC
Ta có:
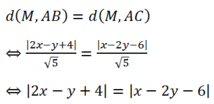

Xét vị trí của B ; C với đường thẳng x+ y+ 10= 0
Có ( -2+ 10) .( -6-2) <0 nên B và C nằm khác phía so với đường thẳng này. Do đó x+ y+10= 0 là phân giác trong.
Vậy đường thẳng cần tìm là 3x – 3y -2= 0.
Đúng 0
Bình luận (0)
Cho tam giác ABC có phương trình các cạnh AB. x+y-1 0; AC: 7x- y+20 và BC: 10x+ y-190. Viết phương trình đường phân giác trong góc A của tam giác ABC. A. 12x+ 4y-3 0 B. 2x-6y+7 0 C. 12x+ 6y+ 5 0 D. 2x+6y-70
Đọc tiếp
Cho tam giác ABC có phương trình các cạnh AB. x+y-1= 0; AC: 7x- y+2=0 và BC: 10x+ y-19=0. Viết phương trình đường phân giác trong góc A của tam giác ABC.
A. 12x+ 4y-3= 0
B. 2x-6y+7= 0
C. 12x+ 6y+ 5= 0
D. 2x+6y-7=0
Đáp án B
Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình

Do đó: B( 2; -1)
Tương tự: tọa độ điểm C( 1; 9)
PT các đường phân giác góc A là:
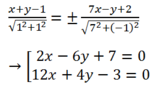
Đặt T1(x; y) = 2x- 6y+ 7 và T2= 12x+ 4y-3 ta có:
T1(B). T1(C) < 0 và T2(B) T2(C) >0.
Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.
Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A,đường cao AH ;HE vuông góc AB;HF vuông góc AC1,CM:AE*ABAF*AC2,CM:tam giác AEF đồng dạng tam giác ACB3,Cho BH8cm;CH18cm.Tính EF?4,M là trung điểm của BC.CM:AM vuông góc EF?5,Cho BC2a cố định .Tìm vị trí của A để S tam giác AHF max6,Đặt ABc;ACb;BCa(a;b;c0);AHh;BEx;CFy(h,x,y0)CM:a,frac{x}{y}frac{c^3}{b^3}b,3h^2+x^2+y^2a^2c,acdot xcdot yh^3P/s:chỉ cần làm câu 5 và 6 thôi nha
Đọc tiếp
Tam giác ABC vuông tại A,đường cao AH ;HE vuông góc AB;HF vuông góc AC
1,CM:AE*AB=AF*AC
2,CM:tam giác AEF đồng dạng tam giác ACB
3,Cho BH=8cm;CH=18cm.Tính EF?
4,M là trung điểm của BC.CM:AM vuông góc EF?
5,Cho BC=2a cố định .Tìm vị trí của A để S tam giác AHF max
6,Đặt AB=c;AC=b;BC=a(a;b;c>0);AH=h;BE=x;CF=y(h,x,y>0)
CM:a,\(\frac{x}{y}=\frac{c^3}{b^3}\)
b,\(3h^2+x^2+y^2=a^2\)
c,\(a\cdot x\cdot y=h^3\)
P/s:chỉ cần làm câu 5 và 6 thôi nha