giúp em bài này vs . khỏi cần vẽ trục tọa độ ạ

Cho hàm số y = f (x) = x² có đồ thị (P) và đường thẳng (d) y = 3x + 4
a. Vẽ (d) và (P) trên cùng hệ trục tọa độ Oxy
b. Tìm tọa độ giao điểm A và B của (d) và (P). Tính di ện tích AOAB(giúp tớ câu này vs ạ
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-3x-4=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;16\right);\left(-1;1\right)\right\}\)
AI GIẢI GIÚP MK BÀI NÀY VS Ạ . MK CẢM ƠN NHÌU
Điểm b(2;-1)thuộc đồ thị hàm số y=ax
a)Xác định điểm a
b)vẽ đồ thị hs y=2x trên cùng hệ trục tọa độ
c)Cminh 2 dồ thị vuông góc
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Giúp em giải bài này vs ạ em đang cần gấp ạ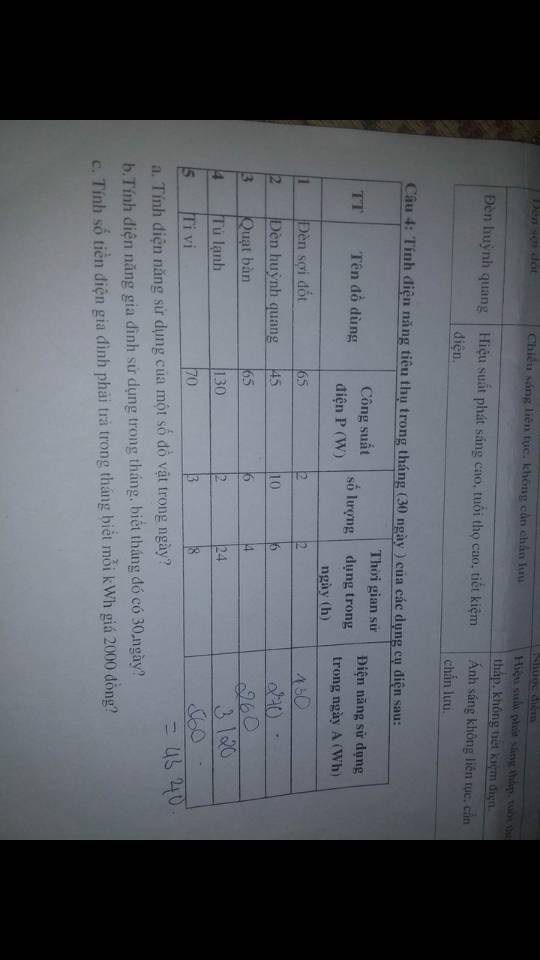
Trong hệ trục Oxy cho 2 điểm M (a-3; b2-4) và N (a-1; b2-3). Đường thẳng Δ qua M,N cắt trục Ox tại điểm P và cắt trục Oy tại điểm Q sao cho diện tích tam giác OPQ bằng \(\dfrac{49}{4}\).Tìm tọa độ của điểm P,Q.
Mn giúp e bài này với ạ.E đang cần gấp ạ.
Trong hệ trục Oxy cho 2 điểm M (a-3; b2-4) và N (a-1; b2-3). Đường thẳng Δ qua M,N cắt trục Ox tại điểm P và cắt trục Oy tại điểm Q sao cho diện tích tam giác OPQ bằng \(\dfrac{49}{4}\).Tìm tọa độ của điểm P,Q.
Mn giúp e bài này với ạ.E đang cần gấp ạ
Trong hệ trục Oxy cho 2 điểm M (a-3; b2-4) và N (a-1; b2-3). Đường thẳng Δ qua M,N cắt trục Ox tại điểm P và cắt trục Oy tại điểm Q sao cho diện tích tam giác OPQ bằng
\(\dfrac{49}{4}\).Tìm tọa độ của điểm P,Q.
Mn giúp e bài này với ạ.E đang cần gấp ạ.
Ủa, cái b2-3 và b2-4 kia là sao em?
Nó là \(b^2-3\) hay \(b_2-3\)?
\(\overrightarrow{MN}=\left(2;1\right)\Rightarrow\) đường thẳng MN nhận (1;-2) là 1 vtpt
Phương trình MN hay \(\Delta\) có dạng: \(x-2y+c=0\) (\(c\ne0\) vì \(\Delta\) cắt 2 trục Ox, Oy tại 2 điểm pb)
Tọa độ P là nghiệm: \(\left\{{}\begin{matrix}y=0\\x-2y+c=0\end{matrix}\right.\) \(\Rightarrow P\left(-c;0\right)\Rightarrow OP=\left|x_P\right|=\left|c\right|\)
Tọa độ Q là nghiệm: \(\left\{{}\begin{matrix}x=0\\x-2y+c=0\end{matrix}\right.\) \(\Rightarrow Q\left(0;\dfrac{c}{2}\right)\Rightarrow OQ=\left|y_Q\right|=\left|\dfrac{c}{2}\right|\)
\(Q_{OPQ}=\dfrac{1}{2}.OP.OQ=\dfrac{c^2}{4}=\dfrac{49}{4}\)
\(\Rightarrow c=\pm7\)
Đề bài chính xác là trục Ox, Oy chứ ko phải tia đúng ko nhỉ? Nếu đề là trục thì lấy cả 2 giá trị +-, đề là tia thì chỉ lấy nghiệm dương
\(\Rightarrow\left\{{}\begin{matrix}P\left(-7;0\right)\\Q\left(0;\dfrac{7}{2}\right)\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}P\left(7;0\right)\\Q\left(0;-\dfrac{7}{2}\right)\end{matrix}\right.\)
Trong hệ trục Oxy cho 2 điểm M (a-3; b2-4) và N (a-1; b2-3). Đường thẳng Δ qua M,N cắt trục Ox tại điểm P và cắt trục Oy tại điểm Q sao cho diện tích tam giác OPQ bằng \(\dfrac{49}{4}\).Tìm tọa độ của điểm P,Q.
Mn giúp e bài này với ạ.E đang cần gấp ạ.