Cho (d) : y = ax+b và (d') : y = cx+d ( a;c khác 0; b khác d)
(d) cắt Ox tại A; (d') cắt Ox tại B ; và (d) cắt (d') tại C
Gọi D là trung điểm của AB
Lập phương trình đường thẳng đi qua C và D
Những câu hỏi liên quan
Hai đường thẳng (d): y = ax + b và (g): y = cx + d song song khi nào?
A. a=c
B. a khác b
C. a = c và b = d
D. a = c và b khác d
Cho (d) : y = ax+b và (d') : y = cx+d ( a;c khác 0; b khác d)
(d) cắt Ox tại A; (d') cắt Ox tại B ; và (d) cắt (d') tại C
Gọi D là trung điểm của AB
Lập phương trình đường thẳng đi qua C và D
Xác định a, b, c, d để đồ thị của các hàm số:
y = x 2 + ax + b
và y = cx + d
cùng đi qua hai điểm M(1; 1) và B(3; 3).
a và b thỏa mãn hệ phương trình :
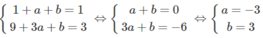
c và d thỏa mãn hệ phương trình:
Đúng 0
Bình luận (0)
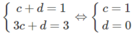
57. Cho hs f(x) = ax +b / cx +d ( a,b,c,d thuộc R , c#0) . Biết f(1)=1 , f(2)=2 và f(f(x))=x với mọi x # -d/c. Tìm tiệm cận ngang của đồ thị hs y = f(x)
\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang
Đúng 0
Bình luận (0)
30 tháng 1 2021 lúc 23:03
Đạo hàm của hàm số \(y=\left(ax+b\right)sinx+\left(cx+d\right)cosx\). tinh \(a+b+2c+d\)?
Hở, là sao nhỉ? Đạo hàm xong nhưng tính a+b+2c+d kiểu gì?
Đúng 0
Bình luận (0)
57. Cho hs f(x) = \(\dfrac{ax+b}{cx+d}\) ( a,b,c,d thuộc R , c#0). Biết f(1)=1 , f(2)=2 và f (f(x)) =x với mọi x # \(\dfrac{-d}{c}\). Tìm tiệm cận ngang của đồ thị hs y= f(x)
cho a;b;c;d;m thuộc tập hợp N*
biết m bằng a nhân d trừ b nhân c và a;b;c lần lượt nguyên tố cùng nhau với m
cmr ax cộng by chia hết cho m khi và chỉ khi cx cộng dy chia hết cho m ( x;y thuộc N* )
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là
A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho biểu thức : M = (ax + by)/( cx + dy) ( c, d khác 0)
CMR: nếu giá trị của biểu thức M không phụ thuộc vào x và y thì 4 số a,b,c,d lập thành một tỉ lệ thức