Cho hai đường tròn (O) và (O’) cắt nhau tại C và D. Một đường thẳng tiếp xúc với (O) và (O’) tại A và B. Đường thẳng CD cắt AB tại M. Chứng minh: MA = MB

Những câu hỏi liên quan
Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O) hẻ hai tiếp tuyến MA,MB của (O) ( với A,B là các tiếp điểm). Kẻ AH vuông góc với MB tại H. Đường thẳng AH cắt (O) tại N ( khác A). Đường tròn đường kính NA cắt các đường thẳng AB và MA theo thứ tự tại I và K. a) Chứng minh tứ giác NHBI nội tiếp. b) Chứng minh tam giác NHI đồng dạng với tam giác NIK. c) Gọi C là giao điểm của NB và HI, gọi D là giao điểm của Na và KI, Đường thẳng CD cắt MA tại E. Chứng minh CI EA.
Đọc tiếp
Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O) hẻ hai tiếp tuyến MA,MB của (O) ( với A,B là các tiếp điểm). Kẻ AH vuông góc với MB tại H. Đường thẳng AH cắt (O) tại N ( khác A). Đường tròn đường kính NA cắt các đường thẳng AB và MA theo thứ tự tại I và K. a) Chứng minh tứ giác NHBI nội tiếp. b) Chứng minh tam giác NHI đồng dạng với tam giác NIK. c) Gọi C là giao điểm của NB và HI, gọi D là giao điểm của Na và KI, Đường thẳng CD cắt MA tại E. Chứng minh CI = EA.
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B (O, O’ thuộc hai nửa mặt phẳng bờ AB). Tiếp tuyến chung gần B của hai đường tròn lần lượt tiếp xúc với (O) và (O’) tại C, D. Qua A kẻ đường thẳng song song với CD lần lượt cắt (O) và (O’) tại M, N (M, N khác A). Các đường thẳng CM và DN cắt nhau tại E. Gọi P và Q lần lượt là giao điểm của đường thẳng MN với đường thẳng BC và đường thẳng BD. Chứng minh rằng:a)Đường thẳng AE vuông góc với đường thẳng CD. b)Tứ giác BCED nội tiếp. c)Tam giác...
Đọc tiếp
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B (O, O’ thuộc hai nửa mặt phẳng bờ AB). Tiếp tuyến chung gần B của hai đường tròn lần lượt tiếp xúc với (O) và (O’) tại C, D. Qua A kẻ đường thẳng song song với CD lần lượt cắt (O) và (O’) tại M, N (M, N khác A). Các đường thẳng CM và DN cắt nhau tại E. Gọi P và Q lần lượt là giao điểm của đường thẳng MN với đường thẳng BC và đường thẳng BD. Chứng minh rằng:a)Đường thẳng AE vuông góc với đường thẳng CD. b)Tứ giác BCED nội tiếp. c)Tam giác EPQ là tam giác cân
cho nửa đường tròn tâm O có đường kính AB=2R. Trên đường tròn O lấy điểm M ( MA<MB) . Tiếp tuyến tại M của O cắt hai tiếp tuyến tại A và B của đường tròn O lần lượt tại C và D a) chứng minh CD = AC+BD b) vẽ đường thẳng BM cắt tia AC tại E và vẽ MH vuông góc với AB tại H Chứng minh OC song song MB và ME.MB=AH.AB c) CM HM là tia phân giác của góc CHD
Cho đường tròn (O) và đường thẳng xy tiếp xúc với đường tròn tại A. Vẽ đường tròn (I) đường kính OA.
a) Chứng minh rằng hai đường tròn (O) và (I) tiếp xúc với nhau
b) Vẽ dây cung AC của (O) cắt I tại một điểm thứ hai là M. Chứng minh MA=MC
c) đường thẳng OM cắt xy tại B. Chứng minh rằng BC là tiếp tuyến của (O)
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại Da, Nêu cách vẽ đường tròn (I) nói trênb, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàngc, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
Đọc tiếp
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D
a, Nêu cách vẽ đường tròn (I) nói trên
b, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàng
c, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
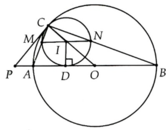
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O'). Đường tròn đường kính OC cắt (O) tại M và N.
a. Đường thẳng CM cắt (O') tại P. Chứng minh OM//BP
b. Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân
= ɬųყɧყ℘
Ŋɧą
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến cắt đường tròn (O) tại C, cắt đường tròn (O') tại D sao cho CD vuông góc với AB, đường thẳng CB cắt đường tròn (O) tại M, đường thẳng DB cắt đường tròn (O') tại N. Chứng minh AB là tia phân giác của góc MAN
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N. a/ Đường thẳng CM cắt (O’) tại P. Chứng minh: OM//BP. b/ Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân.
Từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB với đường tròn (A,B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB và cắt đường tròn tại C ;đoạn thẳng MC cắt đường tròn tại D. Hai đường thẳng AD và MB cắt nhau tại E.
a) CMR: tứ giác MAOB nội tiếp
b) CMR: ∆MED ~ ∆AEM. Từ đó suy ra ME²=ED.AE
c) chứng minh E là trung điểm của đoạn MB
Bài 1: Từ điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB (A,B là tiếp điểm ). Cho biết góc AMB bằng 400a) Tính góc AOBb) Từ O kẽ đường thẳng vuông góc OA cắt MB tại N. Chứng minh tam giác OMN là tam giác cânBài 2 Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn , nó cắt Ax , By lần lượt tai C và Da) chứng minh : Tam giác COD là tam giác vuôngb)Chứng minh : MC.MDOM...
Đọc tiếp
Bài 1: Từ điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB (A,B là tiếp điểm ). Cho biết góc AMB bằng 400
a) Tính góc AOB
b) Từ O kẽ đường thẳng vuông góc OA cắt MB tại N. Chứng minh tam giác OMN là tam giác cân
Bài 2 Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn , nó cắt Ax , By lần lượt tai C và D
a) chứng minh : Tam giác COD là tam giác vuông
b)Chứng minh : MC.MD=OM2
c) Cho biết OC=BA=2R, tính AC và BD theo R
Bài 3 : Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O'). Đường tròn đường kính OC cắt (O) tại M và N
a)Đường thẳng CM cắt (O') tại P Chứng minh : OM////BP
b) Từ C kẽ đường thẳng vuông góc với CM cắt tia ON tại D . Chứng minh : Tam giác OCD là tam giác cân
Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
nên OC là phân giác của góc MOA(1) và CM=CA
Xet (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b:
Xét ΔCOD vuông tại O có OM là đường cao
nên MC*MD=OM^2
c: \(AC=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
Đúng 0
Bình luận (0)















