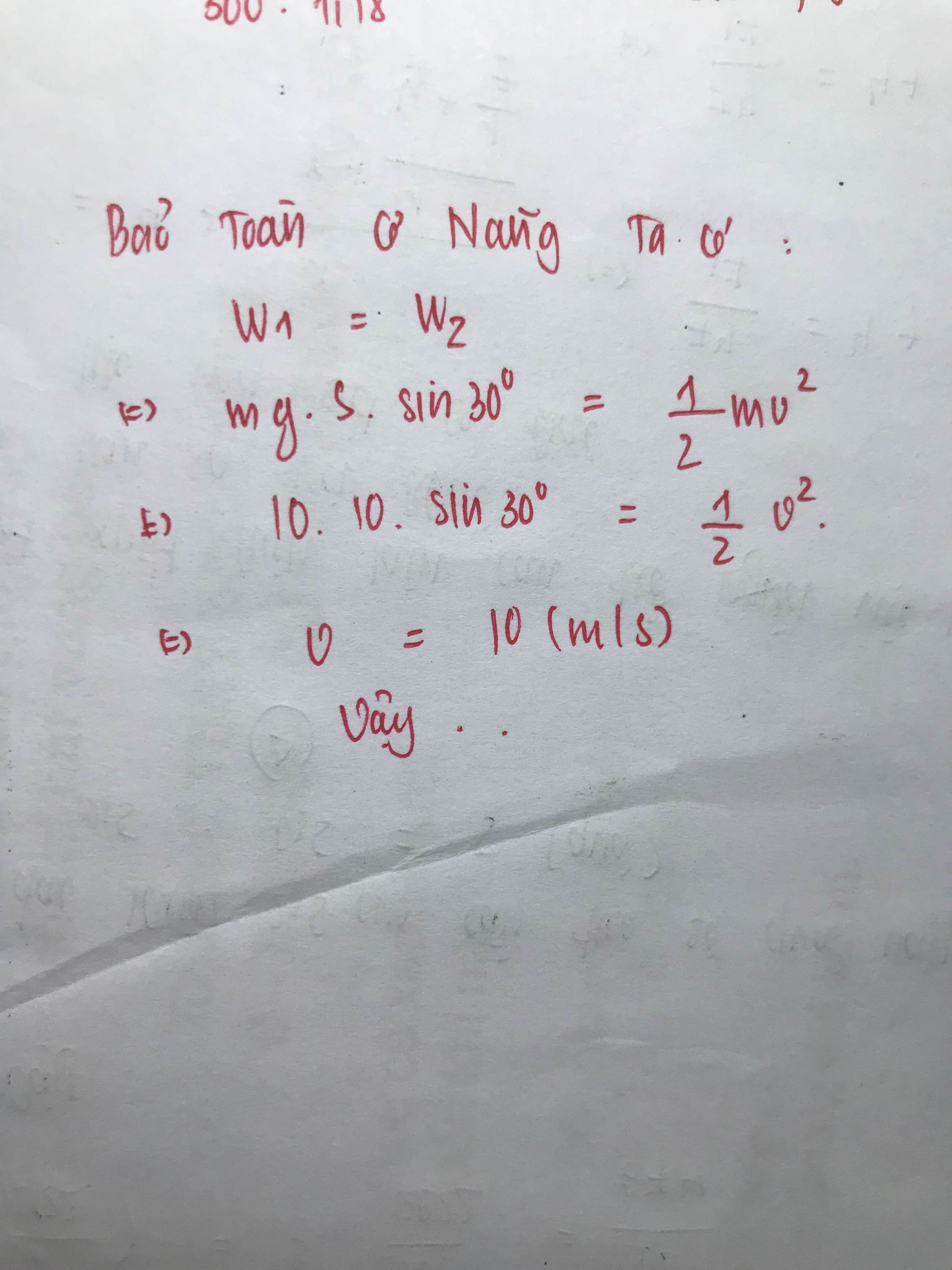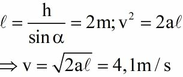Vật có khối lượng 500 g trượt không vận tốc đầu từ đỉnh một mặt phẳng nghiêng cao 20 m. Cho ma sát là không đáng kể. Cho g = 10 \(m/s^2\). Tìm công của trọng lực và vận tốc của vật ở chân dốc.

Những câu hỏi liên quan
Một vật khối lượng 10 kg trượt không vận tốc đầu từ đỉnh của một mặt dốc có độ cao 20 m. Tới chân mặt dốc, vật có vận tốc 15 m/s. Lấy g = 10 m/ s 2 . Xác định công của lực ma sát trên mặt dốc này.
Chọn mặt đất làm gốc tính thế năng ( W t = 0), chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường, hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:
W 2 - W 1 = (m v 2 /2 + mgz) - (m v 0 2 /2 + mg z 0 ) = A m s
Thay số: v 0 = 0, z 0 = 20 m, v = 15 m/s và z = 0, ta tìm được
A m s = m( v 2 /2 - g z 0 ) = 10( 15 2 /2 - 10.20) = -875(J)
Đúng 0
Bình luận (0)
Câu 6. Vật có khối lượng 1kg trượt không vận tốc đầu từ đỉnh một mặt dốc cao 20cm. Khi tới chân dốc thì vật có vận tốc 5m/s. Lấy g = 10 m/s2. Tính công của lực ma sát.
\(20cm=0,2m\)
Lấy chân mặt dốc làm mốc thế năng.
Do có ma sát giữa vật và mặt dốc nên \(W_2-W_1=A_{F_{ms}}\)
\(=>A_{F_{ms}}=\dfrac{mv'^2}{2}-mgh=\dfrac{1\cdot5^2}{2}-1\cdot10\cdot0,2=10,5\left(J\right)\)
Đúng 7
Bình luận (0)
Một vật trượt không vận tốc đầu từ đỉnh dốc dài 10 m, góc nghiêng giữa mặt dốc và mặt phẳng nằm ngang là \(30^o\). Bỏ qua ma sát. Lấy g = 10 m/\(s^2\). Tính vận tốc của vật ở chân dốc?
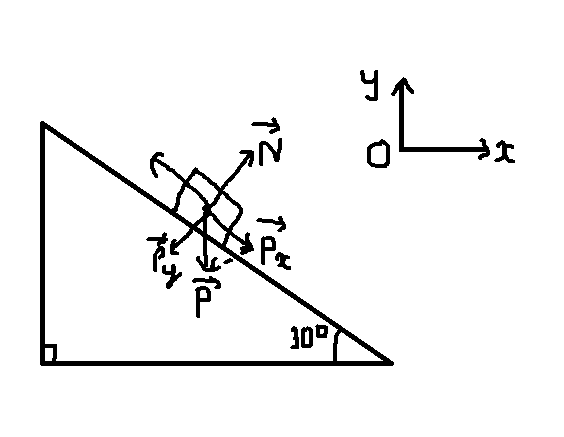
Theo định luật ll Niu tơn:
\(\overrightarrow{P_x}+\overrightarrow{P_y}+\overrightarrow{N}=m\cdot a\)
\(Ox:P=P_x\cdot sin\alpha\Rightarrow m\cdot a=mg\cdot sin30^o\)
\(\Rightarrow a=g\cdot sin30^o=10\cdot sin30^o=5\)m/s2
Vận tốc vật tại chân dốc:
\(v^2-v_0^2=2aS\Rightarrow v=\sqrt{2aS}=\sqrt{2\cdot5\cdot10}=10\)m/s
Đúng 2
Bình luận (0)
Một vật được thả không vận tốc đầu trượt xuống nhanh dần đều từ đỉnh một con dốc dài 25 m, nghiêng một góc 30 0 so với mặt phẳng ngang. Biết lực ma sát bằng 40% trọng lượng của vật. Lấy g = 10 m/s 2 . Tính vận tốc của vật cuối chân dốc và hệ số ma sát trượt giữa vật và mặt nghiêng.
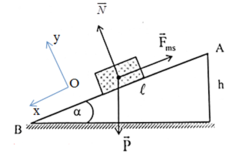
Một vật có khối lượng m = 100g trượt không vận tốc đầu từ đỉnh xuống chân một mặt phẳng nghiêng dài l = 2m, chiều cao h = 0,4m. Vận tốc ở chân mặt phẳng nghiêng là 2m/s. Công của lực ma sát có giá trị là:
A. −0,4J
B. −0,1J
C. −0,8J
D. −0,2J
Lời giải
Chọn chiều dương là chiều chuyển động của vật, gắn hệ trục tọa độ như hình vẽ


Đúng 0
Bình luận (0)
Một vật có khối lượng 10 kg thả không vận tốc đầu từ đỉnh A của mặt phẳng nghiêng nhẵn bóng không ma sát, chiều dài 1,6 m và góc nghiêng so với phương ngang là 30°. Lấy g 10 m/s². a) Tìm vận tốc vật ở chân dốc B.b) Khi đi hết dốc, vật lăn trên mặt phẳng ngang. Thời gian vật chuyển động trên mặt phẳng ngang đến khi dừng lại là 5s và quãng đường vật di chuyển trên mặt phẳng ngang là 11 m. Biết trên mặt phẳng ngang có một đoạn đường CD không có ma sát còn các chỗ khác đều có ma sát với hệ số ma sá...
Đọc tiếp
Một vật có khối lượng 10 kg thả không vận tốc đầu từ đỉnh A của mặt phẳng nghiêng nhẵn bóng không ma sát, chiều dài 1,6 m và góc nghiêng so với phương ngang là 30°. Lấy g= 10 m/s².
a) Tìm vận tốc vật ở chân dốc B.
b) Khi đi hết dốc, vật lăn trên mặt phẳng ngang. Thời gian vật chuyển động trên mặt phẳng ngang đến khi dừng lại là 5s và quãng đường vật di chuyển trên mặt phẳng ngang là 11 m. Biết trên mặt phẳng ngang có một đoạn đường CD không có ma sát còn các chỗ khác đều có ma sát với hệ số ma sát là p = 0,1. Tìm vận tốc trên đoạn đường CD
Một vật có khối lượng 200 g trượt không vận tốc ban đầu từ đỉnh mặt phẳng nghiêng dài 45 √2 cm, nghiêng 45 độ so với phương nằm ngang xuống chân mặt phẳng nghiêng. Cho g 10 m/s ², bỏ qua mọi ma sát trên mặt phẳng nghiêng. a. Tính vận tốc của vật ở chân mặt phẳng nghiêng? b. Tính độ cao của vật khi động năng của vật bằng 3 lần thế năng của vật? c. Giả sử trên mặt phẳng nghiêng có ma sát với hệ số ma sát là 0,2. Tính vận tốc của vật tại chân mặt phẳng nghiêng khi đó? Yêu cầu vẽ hình
Đọc tiếp
Một vật có khối lượng 200 g trượt không vận tốc ban đầu từ đỉnh mặt phẳng nghiêng dài 45 √2 cm, nghiêng 45 độ so với phương nằm ngang xuống chân mặt phẳng nghiêng. Cho g = 10 m/s ², bỏ qua mọi ma sát trên mặt phẳng nghiêng. a. Tính vận tốc của vật ở chân mặt phẳng nghiêng? b. Tính độ cao của vật khi động năng của vật bằng 3 lần thế năng của vật? c. Giả sử trên mặt phẳng nghiêng có ma sát với hệ số ma sát là 0,2. Tính vận tốc của vật tại chân mặt phẳng nghiêng khi đó?
Yêu cầu vẽ hình
Một vật có khối lượng 10 kg thả không vận tốc đầu từ đỉnh A của mặt phẳng nghiêng nhẵn bóng không ma sát, chiều dài 1,6 m và góc nghiêng so với phương ngang là 30°. Lấy g 10 m/s². a) Tìm vận tốc vật ở chân dốc B. b) Khi đi hết dốc, vật lăn trên mặt phẳng ngang. Thời gian vật chuyển động trên mặt phẳng ngang đến khi dừng lại là 5s và quãng đường vật di chuyển trên mặt phẳng ngang là 11 m. Biết trên mặt phẳng ngang có một đoạn đường CD không có ma sát còn các chỗ khác đều có ma sát với hệ số ma...
Đọc tiếp
Một vật có khối lượng 10 kg thả không vận tốc đầu từ đỉnh A của mặt phẳng nghiêng nhẵn bóng không ma sát, chiều dài 1,6 m và góc nghiêng so với phương ngang là 30°. Lấy g= 10 m/s².
a) Tìm vận tốc vật ở chân dốc B.
b) Khi đi hết dốc, vật lăn trên mặt phẳng ngang. Thời gian vật chuyển động trên mặt phẳng ngang đến khi dừng lại là 5s và quãng đường vật di chuyển trên mặt phẳng ngang là 11 m. Biết trên mặt phẳng ngang có một đoạn đường CD không có ma sát còn các chỗ khác đều có ma sát với hệ số ma sát là p = 0,1. Tìm vận tốc trên đoạn đường CD
Cho một vật có khối lượng m trượt không vận tốc đầu từ đỉnh dốc có độ cao 1m, nghiêng một góc α
30
0
so với mặt phẳng nằm ngang. Biết ma sát giữa vật và mặt phẳng là 0,1. Vận tốc cuối chân dốc là? A.
5
m/s B. 4,1m/s C.
3
m/s D.
2
2
m/s
Đọc tiếp
Cho một vật có khối lượng m trượt không vận tốc đầu từ đỉnh dốc có độ cao 1m, nghiêng một góc α = 30 0 so với mặt phẳng nằm ngang. Biết ma sát giữa vật và mặt phẳng là 0,1. Vận tốc cuối chân dốc là?
A. 5 m/s
B. 4,1m/s
C. 3 m/s
D. 2 2 m/s
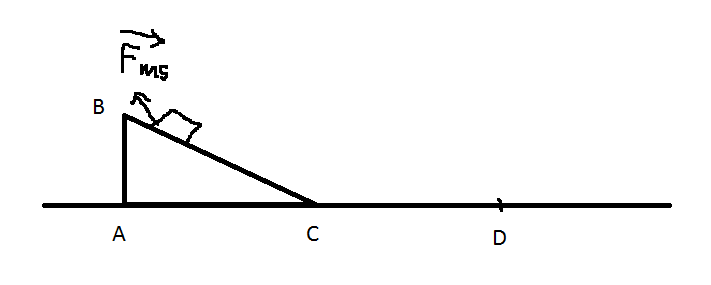
Mọi người giúp mình bài này với ạBài 1: Một vật có khối lượng m1kg trượt không vận tốc ban đầu từ đỉnh B xuống chân dốc C. Cho dốc nghiêng BC cao 10m dài 20m; lấy g10m/s2. Hệ số ma sát giữa vật và mặt phẳng ngiêng là u0,1a: Tính vận tốc của vật ở chân dốc Cb: Đến mặt phẳng ngang vật va chạm mềm với vật M1,5kg đang nằm yên, coi độ lớn vận tốc của vật không thay đổi khi chuyển từ mặt phẳng nghiêng sang mặt phẳng ngang. Sau va chạm hai vật dính vào nhau và chuyển động với cùng vận tốc overrightarro...
Đọc tiếp
Mọi người giúp mình bài này với ạ
Bài 1: Một vật có khối lượng m=1kg trượt không vận tốc ban đầu từ đỉnh B xuống chân dốc C. Cho dốc nghiêng BC cao 10m dài 20m; lấy g=10m/s2. Hệ số ma sát giữa vật và mặt phẳng ngiêng là u=0,1
a: Tính vận tốc của vật ở chân dốc C
b: Đến mặt phẳng ngang vật va chạm mềm với vật M=1,5kg đang nằm yên, coi độ lớn vận tốc của vật không thay đổi khi chuyển từ mặt phẳng nghiêng sang mặt phẳng ngang. Sau va chạm hai vật dính vào nhau và chuyển động với cùng vận tốc \(\overrightarrow{v}\). Tính độ lớn của v
Chú ý: Bài toán phải được giải bằng cách áp dụng các định luật bảo toàn, không dùng phương pháp động lực học
a)Xét tam giác vuông: \(cos\alpha=\dfrac{\sqrt{20^2-10^2}}{20}=\sqrt{3}\)
Độ biến thiên động năng:
\(\Delta A=W_{đC}-W_{đB}=\dfrac{1}{2}m\left(v_C^2-v_B^2\right)=\dfrac{1}{2}mv_C^2\)
Mà \(\Delta A=A_{ms}+A_N+A_P=F_{ms}\cdot s+A_P=-\mu mgscos\alpha+mgh\)
\(\Rightarrow\dfrac{1}{2}mv_C^2=-\mu mgscos\alpha+mgh\Rightarrow\dfrac{1}{2}\cdot1\cdot v_C^2=-0,1\cdot1\cdot10\cdot\sqrt{3}+1\cdot10\cdot10\)
\(\Rightarrow v_C=14,02\)m/s
b)Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v\Rightarrow1\cdot0+1,5\cdot14,02=\left(1+1,5\right)v\)
\(\Rightarrow v=8,412\)m/s
Đúng 2
Bình luận (0)