Tìm các số nguyên x,y biết:
-4/y=x/2
Bài 1.Tìm x,y,z: a.x/5 = -12/20 ; b.2/y = 11/-66 ; c.-3/6 = x/-2 = -18/y = -z/24
Bài 2.Tìm các số nguyên x và y biết : x<0<y và:
-2/x = y/3
Bài 3.Tìm các số nguyên x và y biết x - y = 4 và:
x-3/y-2 = 3/2
Bài 4.Viết dạng chung của tất cả các phân số bằng phân số 21/28
bài 1 tìm các số nguyên x,y biết a)2^x=8
b) 3^4=27
c)(-1,2).x=(-1,2)^4
d)x:(-3/4)=(-3/4)^2
e)(x+1)^3=-125
f)(x-2)^3=64
bài 2 tìm các số nguyên x,y biết
a)(x-1,2)^2=4
d)(x-1,5)^2=9
e)(x-2)^3=64
a) \(2^x=8\)
⇔ \(2^x=2^3\)
⇒ \(x=3\)
b) \(3^x=27\)
⇔ \(3^x=3^3\)
⇒ \(x=3\)
c) \(\left(-\dfrac{1}{2}\right)x=\left(-\dfrac{1}{2}\right)^4\)
⇔ \(x=\left(-\dfrac{1}{2}\right)^4\div\left(-\dfrac{1}{2}\right)\)
⇔ \(x=\left(-\dfrac{1}{2}\right)^3\)
d) \(x\div\left(-\dfrac{3}{4}\right)=\left(-\dfrac{3}{4}\right)^2\)
⇔ \(x=\left(-\dfrac{3}{4}\right)^2\cdot\left(-\dfrac{3}{4}\right)\)
⇔ \(x=\left(-\dfrac{3}{4}\right)^3=-\dfrac{27}{64}\)
d) \(\left(x+1\right)^3=-125\)
⇔ \(\left(x+1\right)^3=\left(-5\right)^3\)
⇔ \(x+1=-5\)
⇔ \(x=-5-1=-6\)
2:
a: (x-1,2)^2=4
=>x-1,2=2 hoặc x-1,2=-2
=>x=3,2(loại) hoặc x=-0,8(loại)
b: (x-1,5)^2=9
=>x-1,5=3 hoặc x-1,5=-3
=>x=-1,5(loại) hoặc x=4,5(loại)
c: (x-2)^3=64
=>(x-2)^3=4^3
=>x-2=4
=>x=6(nhận)
Tìm các số nguyên x;y biết rằng: (x - 2)^2 . (y-3) = -4
\(\left(x-2\right)^2.\left(y-3\right)=-4\\ \rightarrow\left(x-2\right)^2\inƯ\left(4\right),y-3\inƯ\left(4\right).\)
Vì x, y nguyên. Do đó \(\left(x-2\right)^2=1\) hoặc \(\left(x-2\right)^2=4.\)
TH1: \(\left(x-2\right)^2=1\) suy ra x = 1 hoặc x = 3
Khi đó y - 3 = 4 suy ra y = 7.
TH2: \(\left(x-2\right)^2=4\) suy ra x = 4 hoặc x = 0.
Khi đó y - 3 = 1 suy ra y = 4.
Vậy có 4 cặp x, y thỏa mãn là (x, y) = (1, 7); (3, 7); (4, 4); (0, 4)
Lời giải:
Với $x,y$ nguyên thì $(x-2)^2, y-3$ cũng nguyên và $(x-2)^2$ số chính phương nên không âm.
Tích 2 số nguyên bằng $-4$ nên xảy ra các TH sau:
TH1: $(x-2)^2=1; y-3=-4$
$\Rightarrow x=1$ hoặc $x=3; y=-1$. Ta có $(x,y)=(1,-1); (3,-1)$
TH2: $(x-2)^2=4; y-3=-1$
$\Rightarrow x=0$ hoặc $x=4; y=2$. Ta có $(x,y)=(0,2); (4,2)$
tìm các số nguyên x,y biết : x-3/y-2=3/2 và x-y = 4
Theo đề bài ta có: \(\frac{x-3}{y-2}=\frac{3}{2}\Rightarrow2\left(x-3\right)=3\left(y-2\right)\)
\(\Rightarrow2x-6=3y-6\)
\(\Rightarrow2x-3y=-6+6\)
Vì \(x-y=4\Rightarrow x=4+y\)
\(\Rightarrow2\left(y+4\right)-3y=0\)
\(\Rightarrow2y+8-3y=0\)
\(\Rightarrow-y=-8\)
\(\Rightarrow y=8\)
\(\Rightarrow x=y+4=8+4=12\)
Vậy x = 8 và y = 12
Tìm các số nguyên x,y biết x − 3 y − 2 = 3 2 và x − y = 4
Tìm các số nguyên x và y,biết: x-3/y-2=3/2 và x-y=4
x - 3= 3 nên 2(x-3)=3(y-2)
y -2 2
do đó 2x - 6= 3y-6 nên 2x=3y
=> 2x - 2y= y hay 2(x-y)=y
nên 2.4=y
=> 8=y
vì x-y = 4 mà y= 8
=> x = 8+ 4
=> x= 12
Vậy x=12;y=12
Tìm các số nguyên x và y , biết : x - 3 y - 2 = 3 2 và x - y = 4
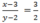 nên 2(x – 3) = 3(y – 2)
nên 2(x – 3) = 3(y – 2)
Do đó 2x – 6 = 3y – 6 nên 2x = 3y
Suy ra 2x – 2y = y hay 2(x – y) = y
Nên 2.4 = y
Vậy y = 8, x = 3y / 2 = 3.8 /2 = 12
Tìm các số nguyên x,y biết : x/4-1/y=1/2
\(\frac{x}{4}-\frac{1}{y}=\frac{1}{2}=\frac{2}{4}\)
\(\Rightarrow\frac{1}{y}=\frac{x-2}{4}\)
=>(x-2)y=4
ta có bảng sau:
| y | -4 | -2 | -1 | 1 | 2 | 4 |
| x-2 | -1 | -2 | -4 | 4 | 2 | 1 |
| x | 1 | 0 | -2 | 6 | 4 | 3 |
vậy (x;y)=(1;-4);(0;-2);(-2;-1);(6;1);(4;2);(3;4)
Tìm các số nguyên x,y biết :x/4 =1/y +1/2
Ta có :\(\frac{1}{y}=\frac{x}{4}-\frac{1}{2}\Rightarrow\frac{1}{y}=\frac{x-2}{4}\)
\(\Rightarrow y\left(x-2\right)=4=4.1=\left(-4\right).\left(-1\right)=\left(-2\right).\left(-2\right)=2.2\)
Vì \(x,y\in Z\Rightarrow\left(x-2\right)\in Z\)
Ta có :
\(y=4;x-2=1\Rightarrow x=3;y=4\)
\(y=1;x-2=4\Rightarrow x=6;y=1\)
\(y=-1;x-2=-;\Rightarrow x=1;y=-4\)
\(y=-1;x-2=-4\Rightarrow x=-2;y=-1\)
\(y=-2;x-2=-2\Rightarrow x=0;y=-2\)
\(y=2;x-2=2\Rightarrow x=4;y=2\)
Câu 1: Tìm số nguyên x;y biết (x - 5) mũ 23 . (y + 2) mũ 7 = 0
Câu 2: Tìm giá trị nhỏ nhất của biểu thức A = (x - 2) mũ 2 + /y + 3/ + 7
Câu 3: Tìm số nguyên x sao cho 5 + x mũ 2 là bội của x + 1
Câu 4: Tìm các số nguyên x;y biết 5 + (x-2) . (y +1) = 0
Câu 5: Tìm x thuộc Z biết x - 1 là ước của x + 2
Câu 6: Tìm số nguyên m để m - 1 là ước của m + 2
Câu 7: Tìm x thuộc Z biết (x mũ 2 - 4) . (7 - x) = 0
Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)
2. \(A=\left(x-2\right)^2+|y+3|+7\)
Ta có :
\(\hept{\begin{cases}\left(x-2\right)^2\ge0\forall x\\|y+3|\ge0\forall y\end{cases}}\)
\(\Rightarrow\left(x-2\right)^2+|y+3|\ge0\forall x;y\)
\(\Rightarrow\left(x-2\right)^2+|y+3|+7\ge7\forall x;y\)
\(\Rightarrow A\ge7\forall x;y\)
Dấu bằng xảy ra
\(\Leftrightarrow\hept{\begin{cases}\left(x-2\right)^2=0\\|y+3|=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-2=0\\y+3=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=-3\end{cases}}}\)
Vậy GTNN của A là 7 khi \(\left(x;y\right)=\left(2;-3\right)\)