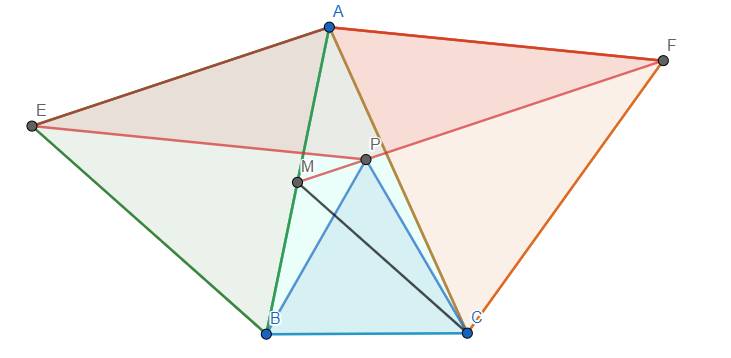
Gọi M là giao điểm của PE với AB.

Ta thấy rằng \(CF=AF=PE,PF=AE=EB\)

Đồng thời \(\widehat{BEP}=60^o-\widehat{AEP}=60^o-\widehat{AFP}=\widehat{PFC}\)

Dẫn đến \(\Delta PBE=\Delta CPF\left(c.g.c\right)\)

\(\Rightarrow PB=PC\)        (1)

Mặt khác, \(\widehat{AMF}=\widehat{MAE}=60^o=\widehat{ACF}\) nên tứ giác AMCF nội tiếp.

\(\Rightarrow\widehat{BAC}=\widehat{PFC}\). Mà lại có \(AB=PF,AC=FC\) nên suy ra \(\Delta ABC=\Delta FPC\left(c.g.c\right)\)

\(\Rightarrow PC=BC\)               (2)

Từ (1) và (2) \(\Rightarrow\Delta PBC\) đều (đpcm)

ta có : góc EBN = góc FCA(1)

lại có : góc EBC = 90 độ ; FCB = 90 độ

=> EBC = FBC (2)

từ (1) và (2) suy ra:

góc PBC = góc PCB

tiếp tục có:

\(\widehat{BPH}+\widehat{CPH}=2.\widehat{EBP}\)

mà \(2.\widehat{EBP}=\widehat{PBC}\)

\(\Rightarrow\widehat{BPH}+\widehat{CPH}=\widehat{PBC}\)

\(mà\widehat{BPH}+\widehat{CPH=}\widehat{BPC}\)

\(\Rightarrow\widehat{PBC}=\widehat{PBC}=\widehat{PCB}\)

từ đó suy ra : tam giác PBC là tam giác đều

( bn không hỉu chỗ nào thì hỏi lại mình nhe)

Theo hình vẽ thì $PBC$ làm sao mà là tam giác đều được nhỉ?

Xét tam giác ABD và tam giác FBC có:

AB=FB ( cạnh tam giác đều FAB)

DB=BC ( cạnh tam giác đều DBC)

góc ABD = góc FBC ( cùng bằng góc ABC + 60 độ)

Suy ra tam giác ABD = tam giác FBC (C.G.C)

=> FC=AD

LẤY I LÀ TRUNG ĐIỂM CỦA BC, O LÀ TRUNG ĐIỂM CỦA AC

XÉT TAM GIÁC MAN VÀ TAM GIÁC IOF CÓ

OI = AB/2=AE/2=AM

OF=AN ( CÚNG LÀ ĐƯƠNG CAO CỦA TAM GIÁC ĐỀU)

GÓC FOI = GÓC MAN = 90 + GÓC A

=> TAM GIÁC MAN = TAM GIACC IOF ( C.G.C)

=> FI = DM

=> GÓC OFI = GÓC MNA

=> GÓC MND = GÓC ANC - GÓC MNA - GÓC DNC

                     = 90 - GÓC OFI - GÓC IFC

                    = 90 - 30 = 60

LẠI CÓ FI = ND/2

           FI = MD

=> MD = ND/2

MÀ GÓC MND = 60

-> TAM GIÁC MND LÀ NỬ TAM GIÁC ĐỀU

=> DM VUÔNG GÓC DN

Hà Minh Hiếu Good !  

????????????????????????????????????????

☺️ ☺️ ☺️ ☺️ ☺️ ☺️

còn cái nịt bạn ơi

tic cái nha do ngoc thanh