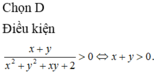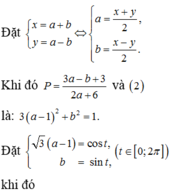Cho hai số thực x và y thõa mãn \(x^2+xy+y^2=1\). Tìm giá trị lớn nhất của \(P=x^3y+y^3x\)

Những câu hỏi liên quan
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
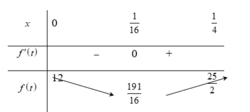
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
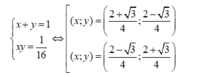
Chọn A.
Đúng 0
Bình luận (0)
Cho hai số thực x, y dương thõa mãn điều kiện x2 + y2 - xy = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức : P = x2 + y2. (Trích đề thi HSG toán 9 tỉnh Bình Định năm học 2012-2013)
(Cho hai số thực dương x,y thõa mãn xy=1. Tìm giá trị nhỏ nhất của biểu thức: M=x2+y2+3/(x+y+1)
Cho x, y là các số thực thỏa mãn \(x^2+y^2+xy=3\).
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : \(P=x^3+y^3-3x-3y\)
Đặt \(x+y=t,t\in\left[-2;2\right]\)
Biến đổi được \(P=-2t^3+6t\)
Xét \(f\left(t\right)=-2t^3+6t\) trên \(\left[-2;2\right]\)
Lập bảng biến thiên
Ta có \(P_{Max}=4\) khi t=1
\(P_{Min}=-4\) khi t= -1
Đúng 0
Bình luận (0)
Cho x,y là các số thực dương thỏa mãn xy+1≤ x. Tìm giá trị lớn nhất của biểu thức Q=\(\dfrac{x+y}{\sqrt{3x^2-xy+y^2}}\)
\(x\ge xy+1\Rightarrow1\ge y+\dfrac{1}{x}\ge2\sqrt{\dfrac{y}{x}}\Rightarrow\dfrac{y}{x}\le\dfrac{1}{4}\)
\(Q^2=\dfrac{x^2+2xy+y^2}{3x^2-xy+y^2}=\dfrac{\left(\dfrac{y}{x}\right)^2+2\left(\dfrac{y}{x}\right)+1}{\left(\dfrac{y}{x}\right)^2-\dfrac{y}{x}+3}\)
Đặt \(\dfrac{y}{x}=t\le\dfrac{1}{4}\)
\(Q^2=\dfrac{t^2+2t+1}{t^2-t+3}=\dfrac{t^2+2t+1}{t^2-t+3}-\dfrac{5}{9}+\dfrac{5}{9}\)
\(Q^2=\dfrac{\left(4t-1\right)\left(t+6\right)}{9\left(t^2-t+3\right)}+\dfrac{5}{9}\le\dfrac{5}{9}\)
\(\Rightarrow Q_{max}=\dfrac{\sqrt{5}}{3}\) khi \(t=\dfrac{1}{4}\) hay \(\left(x;y\right)=\left(2;\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
Cho x,y là 2 số thực thỏa mãn x2+xy2+2xy+3x+3y-4=0
Tìm giá trị lớn nhất, giá trị nhỏ nhất của P=x+y
Mọi người giúp mình nha, mình cần gấp ạ
Cho hai số thực x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Cho hai số thực x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = x + 2 y + 3 x + y + 6
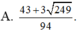
![]()
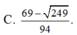
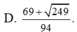
Cho x và y là hai số thực thõa mãn x2 +y2 =4 . Tìm giá trị lớn nhất , nhỏ nhất của biểu thức P=x+y?
Ta có : \(x^2+y^2=4< =>x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
\(< =>4\ge\frac{\left(x+y\right)^2}{2}< =>\left(x+y\right)^2\le4.2=8< =>x+y\le\sqrt{8}\)
Hay \(x+y\le\sqrt{8}\)
Dấu = xảy ra khi và chỉ khi \(x=y=\sqrt{2}\)
Vậy GTLN của P = \(\sqrt{8}\)đạt được khi và chỉ khi \(x=y=\sqrt{2}\)
cho x,y là 2 số thực dương thõa mãn \(x^2+y^2=4\)
Tìm giá trị lớn nhất của biểu thức \(A=\frac{xy}{x+y+2}\)
Bài này hơi căng đấy, theo cách tao nhã nào đó, nó có thể là một bề dày không hoen ố.
Dễ dàng chứng minh được bđt sau:
\(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\) \(\left(i\right)\)
Thật vậy, áp dụng bđt \(B.C.S\) cho bộ số bao gồm \(\left(1;1\right)\) và \(\left(x^2;y^2\right)\) ta được:
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Rightarrow\) \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
Hay nói cách khác, \(\sqrt{2\left(x^2+y^2\right)}\ge x+y\)
Dấu \("="\) xảy ra khi \(x=y\)
Vậy, bđt đã cho được chứng minh!
Theo như cách đề bài đã chọn, để biểu thức \(A\) có giá trị lớn nhất thì \(\frac{1}{A}\) phải đạt giá trị nhỏ nhất hay ta phải tìm \(P_{min}\)(với \(P=\frac{1}{A}\)\(\Rightarrow\) \(P\in Z^+\))
Ta có: \(P=\frac{x+y+2}{xy}=\frac{1}{x}+\frac{1}{y}+\frac{2}{xy}\)
Lại có: \(4=x^2+y^2\ge2xy\) \(\Rightarrow\) \(2\ge xy\) (theo bđt Cauchy cho hai số \(x^2,y^2\) không âm)
nên \(P\ge\frac{1}{x}+\frac{1}{y}+1\)
Mặt khác, tiếp tục áp dụng bđt \(Cauchy-Schwarz\) dạng \(Engel\) cho bộ số gồm \(\left(\frac{1}{x};\frac{1}{y}\right)\) đối với \(P,\)ta có:
\(P\ge\frac{4}{x+y}+1\ge\frac{4}{\sqrt{2\left(x^2+y^2\right)}}+1=\frac{4}{\sqrt{2.4}}+1=\sqrt{2}+1\) (theo bđt \(\left(i\right)\) )
Do đó, \(P_{min}=\sqrt{2}+1\) tức là \(\frac{1}{A}\) đạt giá trị nhỏ nhất là \(\sqrt{2}+1\)
Vậy, dễ dàng suy ra được \(A_{max}=\frac{1}{\sqrt{2}+1}\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(\hept{\begin{cases}x,y>0\\x^2+y^2=4\\x=y\end{cases}\Leftrightarrow}\) \(x=y=\sqrt{2}\)
Đúng 0
Bình luận (0)