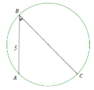
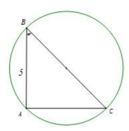
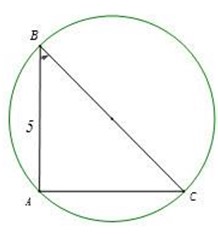
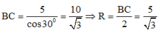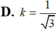cho tam giác ABC vuông tạo A ( AB<AC) có đường cao AH. Vẽ đường tròn tâm B bán kính BA cắt AH tại D. AC, CD là 2 tiếp tuyến của đường tròn (B;BA)
A) Vẽ đường kính AE . từ E vẽ đường thẳng vuông góc với AE cắt AD tại K. Chứng minh \(\frac{ED^2}{2}\)= DK.DH
B) gọi M là giao điểm của ba với đường tròn. từ M vẽ tiếp tuyến với (B) lần lượt cắt AC.CD tại P và Q. Giả sử Sabc = 2Sbpq. chứng minh 3PQ=CP+CQ