Ai giải dùm em bài này em cảm ơn ạ!


 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ
em cảm ơn mọi người nhiều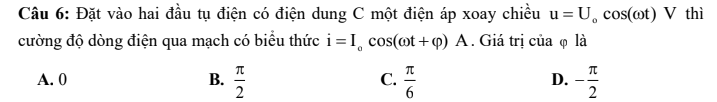
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Phân tích dùm em bài này với ạ. Em cảm ơn trước ạ
Giải dùm em hệ phương trình này với ạ!
em cảm ơn
Lấy \(2.\left(2\right)-\left(1\right)\) ta được:
\(2b+4a+6-\left(a-1-2b\right)=0\)
\(\Leftrightarrow4b+3a+7=0\Rightarrow b=\dfrac{-3a-7}{4}\)
Thế vào (2):
\(\sqrt{a^2+\left(\dfrac{-3a-7}{4}\right)^2}=\dfrac{-3a-7}{4}+2a+3\)
\(\Leftrightarrow\sqrt{25a^2+42a+49}=5a+5\) (\(a\ge-1\))
\(\Leftrightarrow25a^2+42a+49=25a^2+50a+25\)
\(\Rightarrow a=...\Rightarrow b=...\)
giải dùm em cái này vs ạ
em cảm ơn mọi người nhiều
mọi người ai làm gấp dùm em câu này với em cảm ơn ạ!
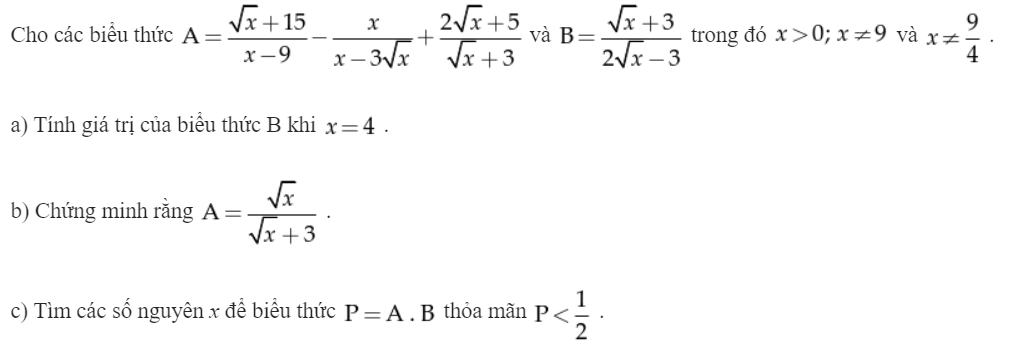
\(a,B=\dfrac{2+3}{2.2+3}=\dfrac{5}{7}\\ b,A=\dfrac{\sqrt{x}+15-x-3\sqrt{x}+2x-\sqrt{x}-15}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\\ c,P=AB=\dfrac{\sqrt{x}}{2\sqrt{x}-3}< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}}{2\sqrt{x}-3}-\dfrac{1}{2}< 0\\ \Leftrightarrow\dfrac{2\sqrt{x}-2\sqrt{x}+3}{2\left(2\sqrt{x}-3\right)}< 0\Leftrightarrow\dfrac{3}{2\left(2\sqrt{x}-3\right)}< 0\\ \Leftrightarrow2\sqrt{x}-3< 0\left(3>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{3}{2}\Leftrightarrow0< x< \dfrac{9}{4}\)
Giải dùm em bài 9 với ạ em cảm ơn
9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)
Ai giải dùm em với ạ. Cảm ơn nhiều ạ!

ai giải giùm em bài này với em cảm ơn ạ.

b: Để hai đường thẳng song song thì m-4=1
hay m=5
\(b,\Leftrightarrow\left\{{}\begin{matrix}m-4=1\\m-1\ne3\end{matrix}\right.\Leftrightarrow m=5\\ c,\Leftrightarrow A\left(3;0\right)\in\left(d_2\right)\Leftrightarrow3m-12+m-1=0\Leftrightarrow m=\dfrac{13}{4}\\ d,\text{PT giao Ox và Oy: }\left\{{}\begin{matrix}y=0\Leftrightarrow x=\dfrac{1-m}{m-4}\Leftrightarrow OA=\left|\dfrac{m-1}{m-4}\right|\\x=0\Leftrightarrow y=m-1\Leftrightarrow OB=\left|m-1\right|\end{matrix}\right.\\ \text{Kẻ }OH\perp\left(d\right)\Leftrightarrow\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-4\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\\ \text{Đặt }OH^2=t\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-8m+17}{m^2-2m+1}\\ \Leftrightarrow m^2t-8mt+17t=m^2-2m+1\\ \Leftrightarrow m^2\left(t-1\right)-2m\left(4t-1\right)+17t-1=0\\ \Leftrightarrow\Delta'=\left(4t-1\right)^2-\left(t-1\right)\left(17t-1\right)\ge0\\ \Leftrightarrow-t^2+10t\ge0\Leftrightarrow0\le t\le10\\ \Leftrightarrow OH_{max}=\sqrt{10}\Leftrightarrow\dfrac{m^2-2m+1}{m^2-8m+17}=10\Leftrightarrow...\)