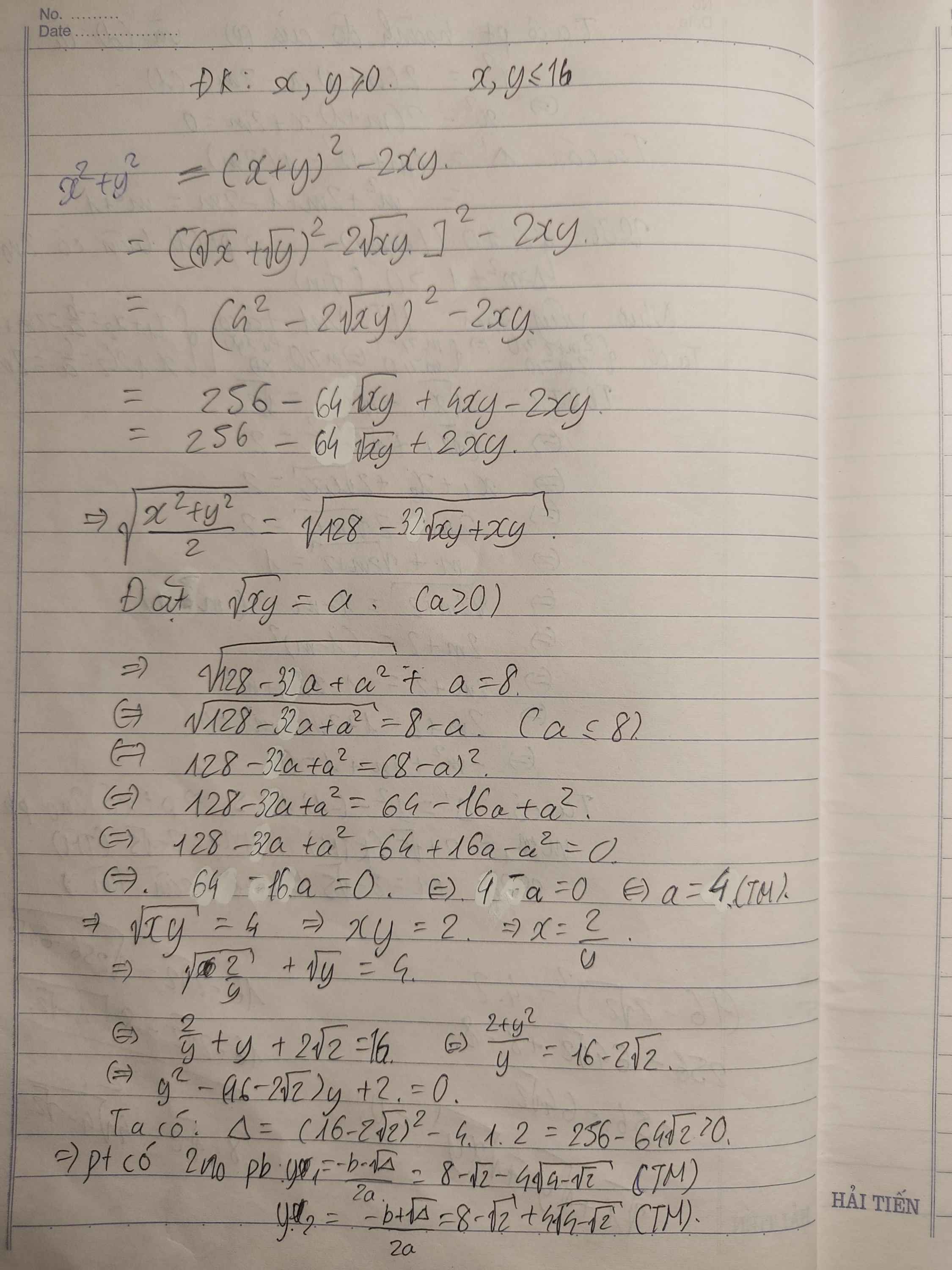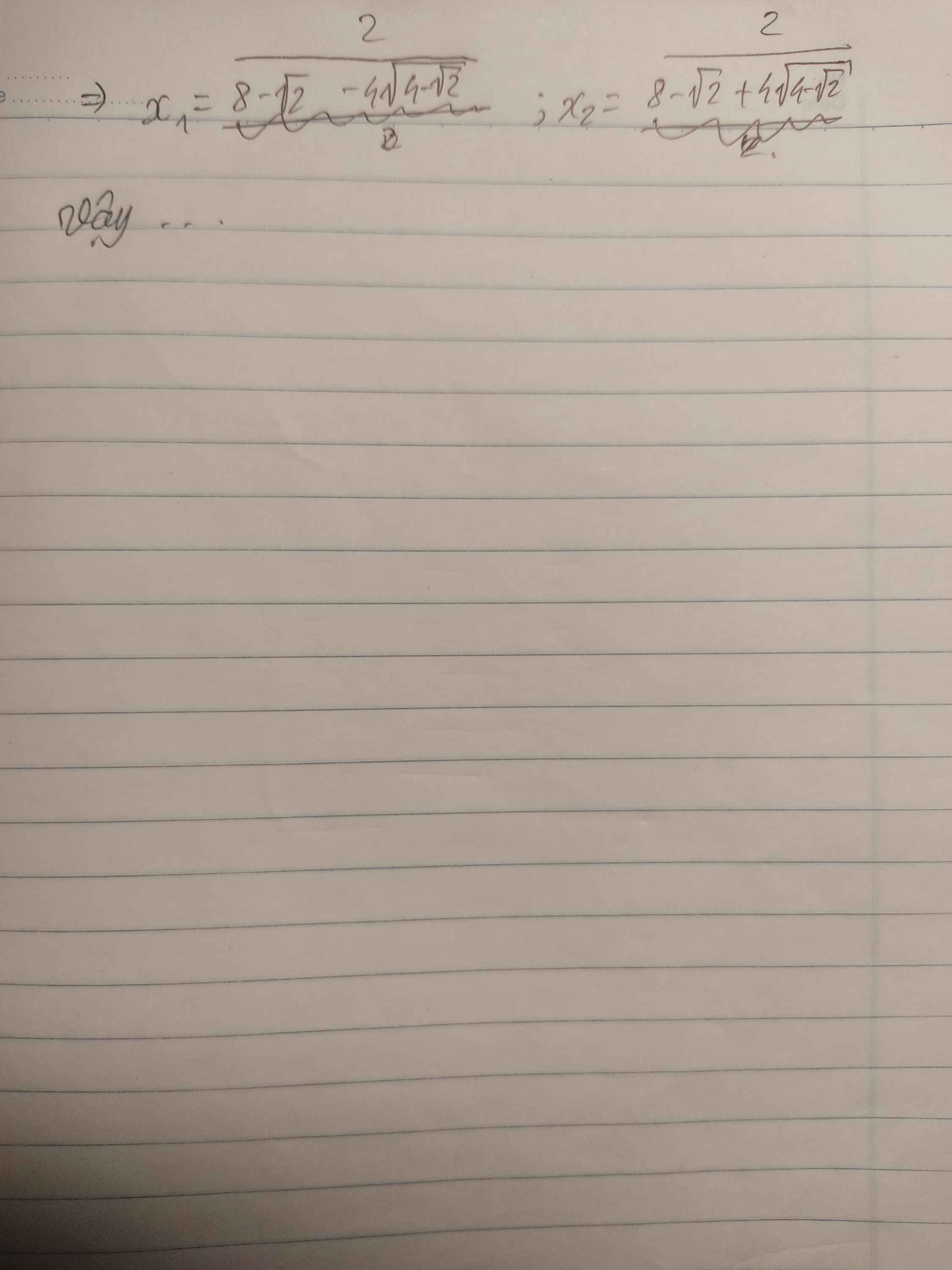bài đây ạ  

3d:

20<x<45

x chia 4 dư 1 nên x-1 thuộc B(4)

=>\(x-1\in\left\{0;4;...;44;48\right\}\)

=>\(x\in\left\{1;5;...;45;49\right\}\)

mà 20<x<45

nên x thuộc {21;26;31;35;41}

4:

a: A={x∈N|51<=x<=127}

b: B={x∈N|100<=x<=999}

c: C={x∈N|x=7k+5; 0<=k<=8}

help plz

1.Điện trở suất của một vật liệu có trị số bằng điện trở của một đoạn dây dẫn hình trụ được làm bằng vật liệu đó có chiều dài 1m và có tiết diện đều là 1m².

2.Điện trở suất đc kí hiệu là \(\rho\)(rô).

3.Đơn vị của điện trở suất là Ôm.mét\(\left(\Omega.m\right)\)

4.Điện trở suất của dây đồng nhỏ hơn.

  Vì vậy dây đồng dẫn điện tốt hơn.

5. Điện trở suất của vật liệu càng nhỏ thì vật liệu đó dẫn điện càng tốt.

lx

lỗi

LX

b: Xét ΔAEB vuông tại E và ΔAKC vuông tại K có 

\(\widehat{EAB}\) chung

Do đó: ΔAEB\(\sim\)ΔAKC

Suy ra: \(\dfrac{AE}{AK}=\dfrac{AB}{AC}\)

hay \(AK\cdot AB=AE\cdot AC\)

Đổi: \(40\%=\dfrac{2}{5}\) 

Số học sinh giỏi Anh bằng : \(1-\dfrac{3}{7}-\dfrac{2}{5}=\dfrac{6}{35}\) (  số học sinh trong câu lạc bộ )

Số học sinh trong câu lạc bộ là:     \(48:\dfrac{6}{35}=280\) ( học sinh )

Số học sinh giỏi Toán là:   \(280.\dfrac{3}{7}=120\) ( học sinh )

Số em giỏi Văn là:   \(280-120-48=112\) ( học sinh )

Bài 4:

Số học sinh của câu lạc bộ là:

\(48:\left(1-\dfrac{3}{7}-\dfrac{2}{5}\right)=48:\dfrac{6}{35}=48\cdot\dfrac{35}{6}=280\)(bạn)

Số học sinh giỏi Toán là:

\(280\cdot\dfrac{3}{7}=120\)(bạn)

Số học sinh giỏi Văn là:

\(280\cdot\dfrac{2}{5}=112\)(bạn)

Câu 6:

Ta có
\(\dfrac{1}{1^2}=1;\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{50^2}< \dfrac{1}{49.50}\)

⇒ A \(=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{50^2}< \) \(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)

⇒ A < \(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)

⇒ A < \(1+\dfrac{99}{100}\)

⇒ A < \(1+\dfrac{99}{100}< 1+\dfrac{100}{100}\)

⇒ A  <  2