Một bàn dài có 2 dãy ghế đối diện nhau. Có bao nhiêu cách xếp n học sinh lớp A và n học sinh lớp B mà 2 học sinh đối diện nhau khác lớp và hai học sinh liên tiếp cũng khác lớp?

Những câu hỏi liên quan
Sắp xếp ngẫu nhiên 5 học sinh lớp 12A và 5 học sinh lớp 12B vào 2 dãy ghế đối diện nhau, mỗi dãy 5 ghế. Tính số cách xếp sao cho hai học sinh ngồi đối diện nhau đều khác lớp.
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một bàn dài gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm có 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới A. B. C. D.
Đọc tiếp
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một bàn dài gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm có 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
Xếp 12 học sinh vào 12 ghế có 12! Cách
![]()
Xếp chỗ ngồi cho 2 nhóm học sinh nam – nữ có 2 cách
Trong nhóm có học sinh nam, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Trong nhóm có học sinh nữ, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Suy ra có ![]() cách xếp thỏa mãn bài toán.
cách xếp thỏa mãn bài toán.
Vậy ![]()
Đúng 0
Bình luận (0)
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một bàn dài gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm có 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giớiB A.
9
4158
B.
9
5987520
C.
9
299760
D.
9
8316
Đọc tiếp
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một bàn dài gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm có 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giớiB
A. 9 4158
B. 9 5987520
C. 9 299760
D. 9 8316
a) Một bàn dài có 2 dãy ghế đối diện nhau, mỗi dãy gồm 6 ghế. Người ta muốn xếp chỗ ngồi cho 6
học sinh trường A và 6 học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách sắp xếp sao cho bất cứ 2 học sinh nào ngồi đối diện nhau thì khác trường với nhau
Xếp 6 học sinh trường A vào 1 dãy ghế: 6! cách
Xếp 6 học sinh trường B vào dãy còn lại: 6! cách
Lúc này hai học sinh đối diện luôn khác trường, có 6 cặp như vậy, mỗi cặp có 2 cách hoán vị nên có \(2^6\) cách hoán vị
Tổng cộng: \(6!.6!.2^6\) cách xếp thỏa mãn
Đúng 5
Bình luận (0)
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một dàn gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới. A.
1
665280
B.
1
462
C.
1
924
D.
3
99920
Đọc tiếp
Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một dàn gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới.
A. 1 665280
B. 1 462
C. 1 924
D. 3 99920

Nam |
Nữ |
Nam |
Nữ |
Nam |
Nữ |
Nữ |
Nam |
Nữ |
Nam |
Nữ |
nam |
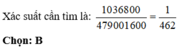
Số cách để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới là: 400.2592 = 1036800 (cách)
Số phần tử của không gian mẫu là: 12! = 479001600
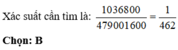
Đúng 0
Bình luận (0)
Một bàn dài có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Người ta muốn xếp chỗ ngồi cho 5học sinh trường X và 5 học sinh trường Y vào bàn nói trên. Tính xác suất để bất cứ hai học sinh nào ngồi đối diện nhau đều khác trường với nhau.
A
.
2
63
B
.
4
63
C
.
8
63
D...
Đọc tiếp
Một bàn dài có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Người ta muốn xếp chỗ ngồi cho 5học sinh trường X và 5 học sinh trường Y vào bàn nói trên. Tính xác suất để bất cứ hai học sinh nào ngồi đối diện nhau đều khác trường với nhau.
A . 2 63
B . 4 63
C . 8 63
D . 5 63
Chọn C
![]()
Ta có số phần tử không gian mẫu: Ω = 10!.
+) Có 10 cách chọn học sinh cho vị trí số 1. Với mỗi cách chọn vị trí số 1 có 5 cách chọn học sinh cho vị trí số 10 ( Nếu vị trí số 1 là học sinh X thì có 5 cách chọn học sinh ở vị trí 10 là học sinh Y và ngược lại).
+) Có 8 cách chọn học sinh cho vị trí số 2 ( Loại 2 học sinh ở vị trí 10) . Với mỗi cách chọn vị trí số 2 có 4 cách chọn học sinh cho vị trí số 9( Nếu vị trí số 2 là X thì có 4 cách chọn vị trí số 9 là Y, chỉ còn 4 do đã loại 1 em ở lần chọn trước).
+) Hoàn toàn tương tự cho đến hết ta được số phần tử của biến cố cần tính xác suất là: ![]()
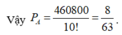
Đúng 0
Bình luận (0)
Có 2 dãy ghế ngồi đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, 3 nam 3 nữ ngồi vô 2 dãy ghế đó s/c mỗi ghế có đúng một học sinh ngồi. Xs để mỗi học sinh nam ngồi đối diện với 1 hs nữ là?
Xép ngẫu nhiên 10 hs gồm 2 hs lớp 12A, 3 hs lớp 12B, 5 hs lớp 12C thành 1 hàng ngang. Xs để 10 hs trên ko có 2 hs nào cùng lớp đứng cạnh nhau là?
Số phần tử của không gian mẫu là n(Ω) = 6!
Gọi A là biến cố 'nam ngồi đối diện nữ.'
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
=> n(A) = 6.4.2.3! = 288
Vậy P(A) = 288/6!
Đúng 0
Bình luận (0)
Một bàn dài có 2 dãy ghế đối diện với nhau, mỗi dãy gồm 6 ghế. Người ta muốn sắp xếp chỗ ngồi cho 6 học sinh trường A và 6 học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách xếp chỗ ngồi trong mỗi trường hợp sau:a) Bất kì 2 học sinh nào ngồi cạnh nhau hoặc đối diện trường khác nhau.b) Bất kì 2 học sinh nào ngồi đối diện nhau thì khác trường nhau
Đọc tiếp
Một bàn dài có 2 dãy ghế đối diện với nhau, mỗi dãy gồm 6 ghế. Người ta muốn sắp xếp chỗ ngồi cho 6 học sinh trường A và 6 học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách xếp chỗ ngồi trong mỗi trường hợp sau:
a) Bất kì 2 học sinh nào ngồi cạnh nhau hoặc đối diện trường khác nhau.
b) Bất kì 2 học sinh nào ngồi đối diện nhau thì khác trường nhau
a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.
Đúng 2
Bình luận (1)
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng A.
2
3
B.
1
3
C.
5
6
D.
1
5
Đọc tiếp
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
A. 2 3
B. 1 3
C. 5 6
D. 1 5














