Tìm khoảng cách giữa 2 điểm A(x1y1)vafB(x2;y2)trong cùng mặt phẳng tọa độ
A,Cho 2014 điểm trong đóko có 3 đ nào thằng hàng .Tính số tam giácđc tạo thành từ 2014 điểm đó
B, Trên tia 0x cho2 điểm A vafB sao cho 0A=a, 0B=a=b . tính khoảng cách giữa các trung điểm của 2 đoạn thẳng OA và OB
cho (P): y = -x^2 và đường thẳng (d): y=2x+m-1
tìm m để (d) cắt (P) tại 2 điểm phân biệt A(x1;x2),B(x2;y2) mà x1y1 -x2y2 -x1x2 = 4
Trả lời:
Phương trình hoành độ giao điểm (P) và (d) ta có:
\(-x^2=2x+m-1\)
\(\Leftrightarrow x^2+2x+m-1=0\)(1)
Ta có: \(\Delta=2^2-4.1.\left(m-1\right)\)
\(=4-4m+4\)
\(=8-4m\)
Để phương trình (1) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow8-4m>0\)
\(\Leftrightarrow4m< 8\)
\(\Leftrightarrow m< 2\)
\(\Rightarrow\)Phương trình (1) có 2 nghiệm phân biệt
\(\Rightarrow\)(d) cắt (P) tại 2 diểm phân biệt \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Áp dụng Vi-ét \(\hept{\begin{cases}x_1+x_2=-2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{cases}}\)
Ta có \(y_1=-x_1^2\); \(y_2=-x_2^2\)
Theo đề bài:
\(x_1.y_1-x_2.y_2-x_1.x_2=4\)
\(\Leftrightarrow x_1.\left(-x_1^2\right)-x_2.\left(-x_2^2\right)-x_1.x_2=4\)
\(\Leftrightarrow-x_1^3+x_2^3-x_1.x_2=4\)
\(\Leftrightarrow-\left(x_1^3-x_2^3\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(x_1^2+x_1.x_2+x_2^2\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-2x_1.x_2+x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(x_1+x_2\right)^2-x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(-2\right)^2-m+1\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(4-m+1\right)=4+m-1\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(3-m\right)=m+3\)
\(\Leftrightarrow-\left(x_1-x_2\right)=\frac{m+3}{3-m}\)
\(\Leftrightarrow x_1-x_2=\frac{m+3}{m-3}\)(3)
Từ (1) (3) ta có: \(\hept{\begin{cases}x_1+x_2=-2\\x_1-x_2=\frac{m+3}{m-3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x_1=-2+\frac{m+3}{m-3}=\frac{9-m}{m-3}=-\left(m+3\right)\\x_1+x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{-\left(m+3\right)}{2}\\x_2=\frac{m-1}{2}\end{cases}}\)
Thay x1, x2 vào (2) ta có
\(x_1.x_2=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}.\frac{m-1}{2}=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}=2\)
\(\Leftrightarrow-\left(m+3\right)=4\)
\(\Leftrightarrow m+3=-4\)
\(\Leftrightarrow m=-7\)(TM)
Vậy \(m=-7\) thì thỏa mãn bài toán
Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết: P( x 1 ; y 1 ), Q( x 2 ; y 2 )
Cho (P):y=x^2 và (d):y=(2m-1)x +8
Chứng minh với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung. Gọi hoành độ của điểm A và B lần lượt là x1 và x2, giả sử x1<x2. Tìm m để tỉ số giữa khoảng cách từ A và B đến trục Oy bằng 4
Xét pt hoành độ gđ của (P) và (d) có:
\(x^2=\left(2m-1\right)x+8\)
\(\Leftrightarrow x^2-\left(2m-1\right)x-8=0\) (*)
Có \(ac=-8< 0\) => pt luôn có hai nghiệm trái dấu
=> (d) luôn cắt (P) tại hai điểm pb có hoành độ trái dấu hay (d) luôn cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung
Hoành độ gđ của A và B là hai nghiệm của pt (*) mà \(x_1< x_2\Rightarrow x_1< 0< x_2\)
Theo viet có: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=-8\end{matrix}\right.\) (|)
Giả sử \(\dfrac{\left|x_1\right|}{\left|x_2\right|}=4\)
\(\Leftrightarrow\dfrac{-x_1}{x_2}=4\)\(\Leftrightarrow x_1+4x_2=0\) (||)
Từ (|), (||) có hệ: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1+4x_2=0\\x_1x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1-2m}{3}\\x_1=\dfrac{4\left(2m-1\right)}{3}\\x_1x_2=-8\end{matrix}\right.\)\(\Rightarrow\dfrac{\left(1-2m\right)}{3}.\dfrac{4\left(2m-1\right)}{3}=-8\) \(\Leftrightarrow\left(1-2m\right)^2=18\)
\(\Leftrightarrow m=\dfrac{1\pm\sqrt{18}}{2}\)
Vậy...
Viết chương trình nhập vào 1 dãy điểm x1y1, x2y2...xn,yn. In các điểm vừa nhập ra màn hình, tính tổng độ dài gấp khúc lần lượt đi qua các điểm thứ 1, 2,..n. Đếm số điểm thuộc góc phần tư thứ 2. Tìm khoảng các xa gốc tọa độ (trục hoành, trục tung) nhất.
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Ta có
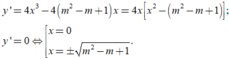
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó 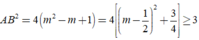
Dấu xảy ra khi m=1/2.
Chọn B.
cho x,y la 2 dai luong ti le nghich,biet x1y1=45,x2=9.tinh x2
Cho Parabol(P) : y=x² và đường thăng (d) : y=(2m-1)x-m+2 ( m là tham số)
A) c)m rằng với mới m đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt
B)Tìm các giá trị m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt A(x1;y1);B(x2;y2) thoả mãn x1y1+x2y2=0
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
\(2m-1=0\Leftrightarrow m=\frac{1}{2}\)\(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x 2 + 2 x x - 1 là
A. - 2 3
B. 2 3
C. 2 15
D. 2 5