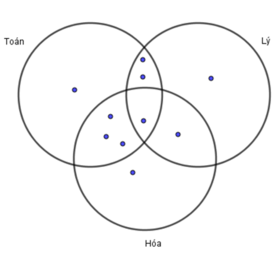
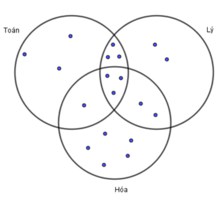
Câu 7. Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hoá, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hoá, 1 học sinh giỏi cả 3 môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá) của lớp 10B1 là:
A. 9 B. 10 C. 18 D. 28