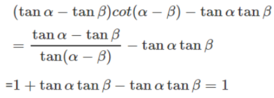Chứng minh định lý α = β biết a // b

Những câu hỏi liên quan
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định
S
1
,
S
2
không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng
M
S
1
,
M
S
2
cắt (α) lần lượt tại
M
1...
Đọc tiếp
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S 1 , S 2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng M S 1 , M S 2 cắt (α) lần lượt tại M 1 và M 2 .
a) Chứng minh rằng M 1 M 2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M 1 M 2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M 1 và M 2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
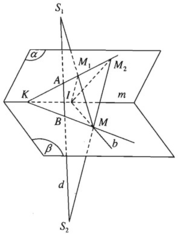
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.
Đúng 0
Bình luận (0)
Cho hàm số �:[�;�]→[�;�]f:[a;b]→[a;b] liên tục trên [�,�][a,b] với ��ab thỏa mãn ∣�(�)−�(�)∣∣�−�∣∣f(α)−f(β)∣∣α−β∣, ∀�,�∈[�;�]∀α,β∈[a;b] phân biệt. Chứng minh rằng ∃!�∈[�;�]:�(�)�∃!γ∈[a;b]:f(γ)γ
(Ở đây kí hiệu ∃!∃! nghĩa là tồn tại duy nhất)
#Toán lớp 11
Đọc tiếp
Cho hàm số liên tục trên với thỏa mãn , phân biệt. Chứng minh rằng
(Ở đây kí hiệu nghĩa là tồn tại duy nhất)
#Toán lớp 11Cho hai mặt phẳng α và β. Một mặt phẳng λ cắt α và β lần lượt theo các giao tuyến a và b. Chứng minh rằng khi a và b cắt nhau tại I thì I là điểm chung của α và β. (h.2.32).
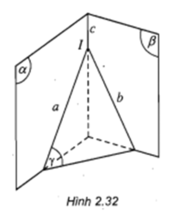
a và b cắt nhau tại I
I ∈ a ∈ α (vì a là giao tuyến của α và λ)
I ∈ b ∈ β ( vì b là giao tuyến của β và λ)
Nên I là điểm chung của α và β
Đúng 0
Bình luận (0)
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.a) Chứng minh ba điểm I, A’, B’ thẳng hàng.b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.
Đọc tiếp
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.
a) Chứng minh ba điểm I, A’, B’ thẳng hàng.
b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.
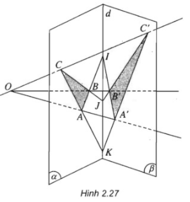
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.
b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.
Đúng 0
Bình luận (0)
Chứng minh: sin α. cos β = sin(α + β) + sin(α − β) 2
* Dựng \(\Delta OAB\)vuông tại A có: \(\widehat{AOB}=\alpha\)
Dựng \(\Delta OBC\)vuông tại B có: \(\widehat{BOC}=\beta\)và OC = 1 (đơn vị độ dài)
Từ C hạ \(CD\perp OA\)tại D \((D\in OA)\)
Từ B hạ \(BH\perp CD\)tại H (\(H\in CD\))
Ta có: \(\widehat{AOB}=\widehat{BCD}=\widehat{BCH}=\alpha\)(góc có cạnh tương ứng vuông góc)
Xét \(\Delta BOC\)có: \(\sin\beta=\frac{BC}{OC}=\frac{BC}{1}\Rightarrow BC=\sin\beta\)
\(\cos\beta=\frac{OB}{OC}=\frac{OB}{1}\Rightarrow OB=\cos\beta\)
Xét \(\Delta OAB\)có: \(\sin\alpha=\frac{AB}{OB}=\frac{AB}{\cos\beta}\Rightarrow AB=\sin\alpha.\cos\beta\)
Xét \(\Delta BCH\)có: \(\cos\alpha=\frac{CH}{BC}=\frac{CH}{\sin\beta}\Rightarrow CH=\cos\alpha.\sin\beta\)
Xét \(\Delta ODC\)có: \(\sin\left(\alpha+\beta\right)=\frac{DC}{OC}=\frac{DC}{1}=DC\)
Mà DC = DH + CH = AB + CH
=> \(\sin\left(\alpha+\beta\right)=\sin\alpha.\cos\beta+\cos\alpha.\sin\beta\)(1)
Cách dựng tương đối giống ở trên khác ở chỗ : OB =1 (đơn vị độ dài), \(\widehat{OCB}=90^o\), \(\widehat{BOC}=\beta,\widehat{AOB}=\alpha-\beta\),\(\widehat{AOC}=\alpha\)
Ta có: \(\widehat{BCH}=\widehat{BCD}=\widehat{AOC}=\alpha\)(góc có cạnh tương ứng vuông góc)
Xét \(\Delta BOC\)có: \(\sin\beta=\frac{BC}{OB}=\frac{BC}{1}=BC\Rightarrow BC=\sin\beta\)
\(\cos\beta=\frac{OC}{OB}=\frac{OC}{1}=OC\Rightarrow OC=\cos\beta\)
Xét \(\Delta OCD\)có:
\(\sin\alpha=\frac{CD}{OC}=\frac{CD}{\cos\beta}\Rightarrow CD=\sin\alpha.\cos\beta\)
Xét \(\Delta BCH\)có:
\(\cos\alpha=\frac{CH}{BC}=\frac{CH}{\sin\beta}\Rightarrow CH=\cos\alpha.\sin\beta\)
Xét \(\Delta OAB\)có:
\(\sin\left(\alpha-\beta\right)=\frac{AB}{OB}=\frac{AB}{1}=AB\)
Mà AB=DH= CD -CH = \(\sin\alpha.\cos\beta-\cos\alpha.\sin\beta\)
=> \(\sin\left(\alpha-\beta\right)=\sin\alpha.\cos\beta-\cos\alpha.\sin\beta\)(2)
Cộng từng vế của (1) và (2) ta được:
\(\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)=2.\sin\alpha.\cos\beta\)=> \(\sin\alpha.\cos\beta=\frac{\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)}{2}\)(đpcm)
Đúng 0
Bình luận (0)
Trong mặt phẳng (
α
) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với (
α
) ta lấy một điểm S tùy ý, dựng mặt phẳng (
β
) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng (
β
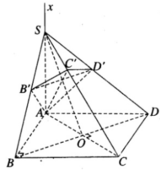
) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Đọc tiếp
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Ta có
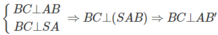
Ta lại có AB′ ⊥ SC nên suy ra AB′ ⊥ (SBC). Do đó AB′ ⊥ B′C
Chứng minh tương tự ta có AD′ ⊥ D′C.
Vậy ∠ ABC = ∠ AB′C = ∠ AC′C = ∠ AD′C = ∠ ADC = 90 °
Từ đó suy ra 7 điểm A, B, C, D, B’, C’, D’ cùng nằm trên mặt cầu đường kính là AC.
Đúng 0
Bình luận (0)
Cho △ ABC vuông tại A, có AB < AC và trung tuyến AM, góc ACB = α, góc AMB = β. Chứng minh rằng (sin α + cos a)2 = 1 + sin β
Cho các góc α, β nhọn. Chứng minh rằng cos(α + β ) = cosαcosβ - sinαsinβ .
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
(tanα - tanβ)cot(α - β) - tanαtanβ