Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S 1 , S 2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng M S 1 , M S 2 cắt (α) lần lượt tại M 1 và M 2 .
a) Chứng minh rằng M 1 M 2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M 1 M 2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M 1 và M 2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
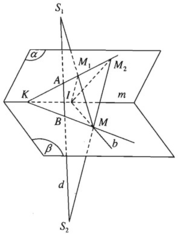
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.