Giải tam giác ABC cân tại A góc C bằng 40°, đường cao BH = 12

Những câu hỏi liên quan
cho tam giác abc đường cao ah biết hc=ab+bh và góc c bằng 40 độ tính các góc của tam giác abc các bạn giải giúp mình với
Cho tam giác ABC cân tại A; đường cao BH; biết BH=h. Giải tam giác ABC
Cho tam giác ABC cân tại A có BH và CK là 2 đường cao.
a) Chứng minh: BH= CK
b) Chứng minh: BCHK là hình thang cân
c) Cho góc BAC = 40 độ. Tính các góc của hình thang
a) Xét ΔKBC và ΔHCB có:
\(\widehat{BKC}=\widehat{CHB}=90\left(gt\right)\)
BC: cạnh chung
\(\widehat{KBC}=\widehat{HCB}\left(gt\right)\)
=> ΔKBC=ΔHCB(ch-gn)
=>BK=HC
b) Có: AB=AK+KB
AC=AH+HC
Mà: AB=AC(gt); BK=HC(gt0
=>AK=AH
=>ΔAKH cân tại A
=>\(\widehat{AKH}=\frac{180-\widehat{A}}{2}\) (1)
Vì ΔABC cân tại A
=>\(\widehat{ABC}=\frac{180-\widehat{A}}{2}\) (2)
Từ (1)(2) suy ra: \(\widehat{AKB}=\widehat{ABC}\) . Mà hai góc này ở vị trí đồng vị
=> KH//BC
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)
=>BCHK là hình thang cân
Đúng 0
Bình luận (0)
a) ta có tam giác ABC cân tại A => hai đường cao BH vafCK cũng bằng nhau
b) ta có tam giác HBC = tam gác KCB
=> BK=CH
mặt khác KH//BC
=> BCHK là hình thang cân
c) góc BAC=40
=> B=C=(180-40):2=70
ta có K+B=180
=> K=H=180-70=110
Đúng 0
Bình luận (0)
cho ABC vuông tại A có BC dài 20cm, góc C bằng 40°. Đường cao AH hãy Tính AB,AC,AH,BH và diện tích tam giác ABC
Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, ∠ C = α
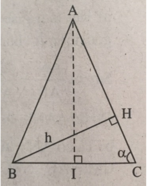
∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được
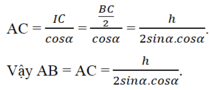
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, đường cao AH (H thuộc BC)
a. tam giác AHB có bằng tam giác AHC không?vì sao?
b. cho góc BAH có số đo bằng 35 độ. tính số đo góc CAH?
c. cho BH=4cm. tính độ dài đoạn thẳng CH?
`a,`
Vì `\Delta ABC` cân tại A:
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$.
Xét `\Delta AHB` và `\Delta AHC` :
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao})$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
Mà $\widehat {BAH} = 35^0$
`->` $\widehat {BAH} = \widehat {CAH} = 35^0.$
`c,`
`\Delta AHB = \Delta AHC (a)`
`-> \text {BH = CH (2 cạnh tương ứng)}`
Mà `\text {BH = 4 cm}`
`-> \text {BH = CH = 4 cm}`
Đúng 3
Bình luận (0)
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: góc CAH=góc BAH=35 độ
c: HC=HB=4cm
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A,đường trung tuyến AM và đường cao BH cắt nhau tại O.Phân giác góc ACH cắt AM tại I,BH giao AB=B'.Tính góc AB'I ?
Cho tam giác ABC cân tại A, góc A>90 độ, đường cao BH, BD là tia phân giác của góc ABH. chứng minh BH>CD.
Cho tam giác ABC cân tại A, góc A>90 độ, đường cao BH, BD là tia phân giác của góc ABH. chứng minh BH>CD.
















