Cho tam giác có số đo ba cạnh ab ; bc ; ca biết chu vi hình tam giác là abc . Tìm số đo các cạnh?

Những câu hỏi liên quan
Cho tam giác ABC có ba cạnh AB, AC, BC lần lượt là 2cm, 3cm, 4cm. Kẻ đường cao AH. Tính
a) Độ dài các đoạn thẳng BH, CH, AH.
b) Độ dài đường cao ứng với cạnh AB, AC
c) Số đo các góc A , B , C của tam giác ABC ( làm tròn đến phút )
a: Nửa chu vi tam giác ABC là:
\(\dfrac{2+3+4}{2}=4,5\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{4,5\left(4,5-2\right)\left(4,5-3\right)\left(4,5-4\right)}\)
\(=\sqrt{4,5\cdot2,5\cdot1,5\cdot0,5}=\dfrac{3\sqrt{15}}{4}\)(cm2)
=>\(\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{3\sqrt{15}}{4}\)
=>\(2\cdot AH=\dfrac{3\sqrt{15}}{4}\)
=>\(AH=\dfrac{3\sqrt{15}}{8}\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB^2+\dfrac{135}{64}=4\)
=>\(HB^2=\dfrac{121}{64}\)
=>HB=11/8(cm)
HB+HC=BC
=>HC+11/8=4
=>HC=4-11/8=21/8(cm)
b: Gọi BK,CE lần lượt là các đường cao ứng với các cạnh AC,AB
Vì BK\(\perp\)AC và CE\(\perp\)AB
nên \(S_{ABC}=\dfrac{1}{2}\cdot BK\cdot AC=\dfrac{1}{2}\cdot CE\cdot AB\)
=>\(\left\{{}\begin{matrix}BK\cdot\dfrac{3}{2}=\dfrac{3\sqrt{15}}{4}\\CE\cdot1=\dfrac{3\sqrt{15}}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BK=\dfrac{\sqrt{15}}{2}\left(cm\right)\\CE=\dfrac{3\sqrt{15}}{4}\left(cm\right)\end{matrix}\right.\)
c: Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{4+9-16}{2\cdot2\cdot3}=\dfrac{-1}{4}\)
=>\(\widehat{BAC}\simeq104^029'\)
Xét ΔABH vuông tại H có \(sinB=\dfrac{AH}{AB}=\dfrac{3\sqrt{15}}{16}\)
=>\(\widehat{B}\simeq46^034'\)
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+104^029'+46^034'=180^0\)
=>\(\widehat{ACB}=28^057'\)
Đúng 0
Bình luận (0)
Tam giác có số đo ba cạnh là : ab ; bc và ca , biết chu vi của tam giác là abc, tìm số đo các cạnh .
Cho tam giác ABC vuông tại A có AB>AC . Trên cạnh BA lấy điểm D sao cho BD=AC .Trên cạnh AC lấy điểm E sao cho CE=AD , CD cắt BE tại O .Trên đường vuông góc với AB tại O lấy điểm F sa cho BF=CE ( F,C thuộc bờ AB)
a, Chứng minh rằng tam giác BDF= tam giác ACD
b, Chứng minh tam giác CDF vuông cân
c, Tính số đo góc COE
Cho tam giác ABC có góc A bằng 60 độ và AB AC.Trên cạnh AC lấy điểm D sao cho AD AB. Gọi H là trung điểm BD.a)Chứng minh: tâm giác AHB tam giác AHDb)Tính số đo góc ABD?c)Trên tia đối của tia BA lấy điểm E sao cho BE DC.Chứng minh AH vuông với EC.
Đọc tiếp
Cho tam giác ABC có góc A bằng 60 độ và AB <AC.Trên cạnh AC lấy điểm D sao cho AD= AB. Gọi H là trung điểm BD.a)Chứng minh: tâm giác AHB= tam giác AHDb)Tính số đo góc ABD?c)Trên tia đối của tia BA lấy điểm E sao cho BE= DC.Chứng minh AH vuông với EC.
a: Xét ΔAHB và ΔAHD có
AH chung
HB=HD
AB=AD
Do đó: ΔAHB=ΔAHD
b: Xét ΔABD cân tại A có \(\widehat{BAD}=60^0\)
nên ΔABD đều
hay \(\widehat{ABD}=60^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tổng số đô hai cạnh AB và AC là 420mm. Tổng số đo hai cạnh AC và BC là 54cm.Tổng số đo hai cạnh BC và AB là 4dm 8cm
a)Tính chu vi tam giác ABC
b) tính số đo mỗi cạnh của hình tam giác đó
Cho tam giác abc có góc bac bằng 90 độ góc abc bằng 50 độ. Bd là phân giác góc abc. Trên cạnh bc lấy e sao cho be bằng ba A, tímh số đo góc c B, chứng minh tam giác bda bằng tam giác bde C, vẽ đường thẳng d vuông góc với ab tại b. Qua a kẻ đường song song bd và cắt d tại m chứng minh am bằng bd
bạn viêt khó hiểu quá, bạn viết lại cho đúng nha
Đúng 0
Bình luận (0)
Một hình tam giác có số đo cạnh thứ nhất là : 43,85 dm ;cạnh thứ hai là 257,8 cm và cạnh thứ ba là 1,3495 m . Tính chu ci tam giác đó với số đo là xăng - ti - mét .
đổi 43,85 dm = 438,5 cm ; 1,3495 m = 134,85 cm
chu vi hình tam giác đó là :
438,5 + 134,85 + 257,8 = 831,15 ( cm )
Đáp số : 831,15 cm
Đúng 0
Bình luận (0)
Một hình tam giác có số đo cạnh thứ nhất là: 43,85dm; cạnh thứ hai là 257,8cm và cạnh thứ ba là 1,3495m. Tính chu vi tam giác đó với số đo là xăng-ti-mét.
Trả lời:
Chu vi tam giác đó là: ................. cm.
Trên ba cạnh AB,AC và CA của tam giác đều ABC lấy các điểm theo thứ tự M,N,P sao cho AM=CN=CP.Gọi O là giao điểm ba đường trung trực của tam giác ABC
a) Tính số đo góc MAO
b)Chứng minh tam giác MAO = tam giác OPC
c)Chứng minh O là giao điểm ba đường trung trực của tam giác ABC
(Nếu được thì cho mình xin hình luôn nhé)
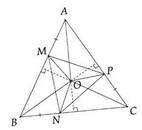
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP
Đúng 0
Bình luận (0)

















