Trong hình vuông cạnh 4cm cho 33 điểm phân biệt mà ko có 3 điểm nào thẳng hàng. Vẽ các đường tròn tâm là các điểm đã cho và bán kính=√2. Chứng minh rằng có 3 điểm nằm trong phần chung 3 đường tròn có tâm là 3 điểm đó.

Những câu hỏi liên quan
Trong hình vuông cạnh 4cm cho 33 điểm phân biệt mà ko có 3 điểm nào thẳng hàng. Vẽ các đường tròn tâm là các điểm đã cho và bán kính=\(\sqrt{2}\). Chứng minh rằng có 3 điểm nằm trong phần chung 3 đường tròn có tâm là 3 điểm đó.
Ta chia hình vuông đề cho thành 16 hình vuông nhỏ bằng nhau (như hình vẽ)

Ta được độ dài cạnh của hình vuông nhỏ là 1
Có 33 điểm đặt vào 16 hình vuông theo nguyên lí Dirichlet
Suy ra tồn tại một hình vuông nhỏ chứa ít nhất 3 điểm
Giả sử hình vuông nhỏ đó là: ABCD (AC cắt BD tại O)
Có \(OA=\frac{AC}{2}=\frac{\sqrt{AB^2+BC^2}}{2}=\frac{\sqrt{1^2+1^2}}{2}=\frac{\sqrt{2}}{2}\)\(\Rightarrow AC=BD=\sqrt{2}\)
Giả sử 3 điểm đó trùng với 3 trong 4 đỉnh bất kì của hình vuông ABCD thì phần chung của ba hình tròn chứa toàn bộ hình vuông và như vậy đã tồn tại 3 điểm thỏa mãn yêu cầu bài toán.
Nếu trong 3 điểm có điểm nằm bên trong hình vuông thì phần chung của ba hình tròn cũng chứa toàn bộ hình vuông và như vậy đã tồn tại 3 điểm thỏa mãn yêu cầu bài toán
KL: tồn tại 3 điểm trong các điểm đã cho thỏa mãn yêu cầu bài toán.
Khó thế này ai lm đc
Cho 81 điểm phân biệt nằm trong một hình vuông có cạnh bằng 1. Chứng minh rằng tồn tại 6 điểm trong các điểm đã cho nằm trong một đường tròn có bán kính bằng 1/5
Các bạn cop mạng cx đc
Cho 81 điểm phân biệt nằm trong một hình vuông có cạnh bằng 1. Chứng minh rằng tồn tại 6 điểm trong các điểm đã cho nằm trong một đường tròn có bán kính bằng \(\frac{1}{5}\)
trong mặt phẳng cho 2n+1 điểm phân biệt ko có 3 điểm nảo thẳng hàng. biết rằng bất kỳ 3 điểm trong các điểm đã cho luôn có 2 điểm có khoảng cách <1.CMR tồn tại 1 hình tròn bán kính 1cm chứa n+1 điểm trong 2n+1 điểm đã cho
Gọi \(2n+1\) điểm đó là \(A_1,A_2,...,A_{2n+1}\). Do số điểm là hữu hạn nên tồn tại 1 đoạn thẳng \(A_iA_j\left(i\ne j\right)\) sao cho \(A_iA_j\) lớn nhất trong các \(A_kA_l\left(k\ne l;k,l=\overline{1,2n+1}\right)\).
TH1: Nếu \(A_iA_j\le1\), ta dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Dĩ nhiên nếu có bất kì điểm \(A_m\) nào nằm ngoài 2 đường tròn trên thì mâu thuẫn với giả thiết \(A_iA_j\) là đoạn thẳng có độ dài lớn nhất. Do đó, tất cả \(2n+1\) điểm sẽ nằm trong 2 đường tròn. Theo nguyên lí Dirichlet sẽ tồn tại 1 hình tròn chứa \(n+1\) điểm trong \(2n+1\) điểm đã cho. Đó là hình tròn cần tìm.
TH2: Nếu \(A_iA_j>1\), ta vẫn dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Khi đó nếu có bất kì điểm \(A_m\) nào nằm ở ngoài cả 2 hình tròn thì \(A_mA_i\) và \(A_mA_j\) đều lớn hơn 1. Khi đó bộ 3 điểm \(\left(A_i,A_j,A_m\right)\) mâu thuẫn với giả thiết trong 3 điểm bất kì luôn có 2 điểm có khoảng cách nhỏ hơn 1. Do vậy, tất cả các điểm đã cho đều nằm trong 2 đường tròn kể trên. Lại theo nguyên lí Dirichlet thì tồn tại \(n+1\) điểm thuộc cùng một hình tròn. Đấy chính là hình tròn cần tìm.
Vậy trong mọi trường hợp, ta đều tìm được 1 hình tròn bán kính 1cm chứa \(n+1\) điểm trong số \(2n+1\) điểm đã cho. Ta có đpcm.
Đúng 1
Bình luận (0)
Mình giải thích thêm trường hợp 1 nhé. Nếu như có 1 điểm \(A_m\) nằm ngoài 1 trong 2 đường tròn \(\left(A_i,1\right)\) và \(\left(A_j,1\right)\) thì 1 trong 2 đoạn \(A_mA_i\) và \(A_mA_j\) sẽ lớn hơn 1. Không mất tính tổng quát, giả sử đó là đoạn \(A_mA_i\). Khi đó \(A_mA_i>1\ge A_iA_j\), vô lí vì ta đã giả sử \(A_iA_j\) là đoạn có độ dài lớn nhất.
Đúng 1
Bình luận (0)
Bài 9. Cho 11 điểm đôi một phân biệt thoả mãn:
i) Không có ba điểm nào thẳng hàng;
ii) Không có bốn điểm nào cùng nằm trên một đường tròn.
Chứng minh rằng có thể vẽ được một đường tròn đi qua ba điểm trong các điểm đã cho và chứa đúng 6 điểm bên trong.
1. Cho đường tròn (A;1cm) và (B;1cm). Điểm A nằm trên đường tròn tâm B. Gọi C là điểm nằm trên cả 2 đường tròn tâm A và tâm B. Giải thích tại sao ABBCCA.2. Cho đoạn thẳng AB4cm. Hãy nêu cách vẽ điểm M sao cho MA3cm, MB2cm.3. Cho đoạn thẳng Ab4cm. Gọi O là trung điểm của nó. Vẽ đường tròn (O;1cm) cắt đoạn OA tại M, cắt đoạn OB tại N.a) Điểm M có là trung điểm của đoạn OA không?b) Điểm N có là trung điểm của đoạn OB không?c) Vẽ đường tròn có tâm trên đoạn thẳng AB có bán kính 2cm sao cho điểm M nằ...
Đọc tiếp
1. Cho đường tròn (A;1cm) và (B;1cm). Điểm A nằm trên đường tròn tâm B. Gọi C là điểm nằm trên cả 2 đường tròn tâm A và tâm B. Giải thích tại sao AB=BC=CA.
2. Cho đoạn thẳng AB=4cm. Hãy nêu cách vẽ điểm M sao cho MA=3cm, MB=2cm.
3. Cho đoạn thẳng Ab=4cm. Gọi O là trung điểm của nó. Vẽ đường tròn (O;1cm) cắt đoạn OA tại M, cắt đoạn OB tại N.
a) Điểm M có là trung điểm của đoạn OA không?
b) Điểm N có là trung điểm của đoạn OB không?
c) Vẽ đường tròn có tâm trên đoạn thẳng AB có bán kính 2cm sao cho điểm M nằm bên trong đường trong, điểm N nằm bên ngoài đường tròn.
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E a)CMR: CD vuông góc với AB , BE vuông góc với AC b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BCBài 3:Cho hình thang ABCD , AB//CD, ABCD , có góc Cgóc D60 độ , CD2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường trò...
Đọc tiếp
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E
a)CMR: CD vuông góc với AB , BE vuông góc với AC
b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC
Bài 3:Cho hình thang ABCD , AB//CD, AB<CD , có góc C=góc D=60 độ , CD=2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường tròn. Tính diện tích đường tròn đó biết CD=4cm
Bài 4:Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E . Gọi M, N, P, Q lần lượt là trung điểm của DE , EB, BC, CD. Chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
@ Trần Ngọc Huyền @ Em lần sau nhớ chia bài ra đăng nhiều lần nhé! .
Đúng 0
Bình luận (0)
Đồng ý với cô Nguyễn Thị Linh Chi
Đăng nhiều thế mới nhìn đã choáng
vẽ một hình tròn có bán kính 2 cm. Trong hình tròn có 2 đường thẳng giao nhau tại tâm đường tròn O, P, Q,E ĐƯỜNG THẲNG 1. Đường thẳng đi qua 2 điểm . 2 đường thẳng nào cắt nhau. chỉ ra các điểm ko thẳng hàng
Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI 1cm, AO 4cm, BP 4cm.a) Vẽ đường (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?b) Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).c) Vẽ đường tròn (I; 1cm)? Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
Đọc tiếp
Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB = 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI =1cm, AO = 4cm, BP = 4cm.
a) Vẽ đường (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?
b) Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Vẽ đường tròn (I; 1cm)? Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
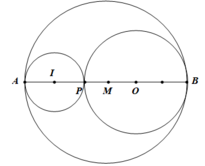
a) Điểm P, O nằm giữa A và B, AO = 4cm, BP = 4cm nên PO = 2cm, BO = 2cm.
Vậy điểm P có nằm trên đường tròn (O; 2cm).
b) Gọi M là trung điểm của AB =>AM = 3cm.
Lại có AI = 1cm => IM = 2cm
=> điểm I nằm trong đường tròn có đường kính AB ( do IM < AM ).
Có OI = 3cm > OP = 2cm nên điểm I nằm ngoài đường tròn (O; 2cm).
Vậy điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Đường tròn (I; 1cm) tiếp xúc với các đường tròn(O; 2cm) và đường tròn có đường kính AB
vì AP + PB = AB
Đúng 0
Bình luận (0)
Câu 72. Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI 1cm, AO 4cm, BP 4cm.a. Vẽ đường tròn (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?b. Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).c. Vẽ đường tròn (I; 1cm). Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
Đọc tiếp
Câu 72. Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB = 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI = 1cm, AO = 4cm, BP = 4cm.
a. Vẽ đường tròn (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?
b. Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c. Vẽ đường tròn (I; 1cm). Đường tròn này tiếp xúc các đường tròn nào? Vì sao?





















