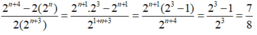Rút gọn: \(S=C^0_{2n} +3^2C^2_{2n}+3^4C^4_{2n}+...+3^{2n}C^{2n}_{2n}\)

Những câu hỏi liên quan
Tính tổng: a) \(S=2C^2_{2n}+4C^4_{2n}+6C^6_{2n}+...+2nC^{2n}_{2n}\)
b) \(S=\dfrac{1}{2}C^0_{2n}+\dfrac{1}{4}C^2_{2n}+\dfrac{1}{6}C^4_{2n}+...+\dfrac{1}{2n+2}C^{2n}_{2n}\)
chứng minh rằng
\(C^0_{2n}+2^2C^2_{2n}+...+2^{2n}C^n_{2n}=\frac{3^{2n}+1}{2}\)
Chứng minh rằng:
\(C^0_{2n}+C^1_{2n}+C^2_{2n}+...+C^{2n}_{2n}=4^n\)
Xét khai triển: \(\left(x+1\right)^{2n}=C_{2n}^0+C_{2n}^1x+C_{2n}^2x^2+...+C_{2n}^{2n}x^{2n}\)
Thay \(x=1\) ta được:
\(2^{2n}=C_{2n}^0+C_{2n}^1+...+C_{2n}^{2n}\)
\(\Leftrightarrow4^n=C_{2n}^0+C_{2n}^1+...+C_{2n}^{2n}\)
Đúng 0
Bình luận (0)
Chứng minh rằng :
\(C_{2n}^0+C^2_{2n}+...+C^{2n}_{2n}=C^1_{2n}+C^3_{2n}+...+C^{2n-1}_{2n}\)
Xét khai triển:
\(\left(x-1\right)^{2n}=C_{2n}^0-C_{2n}^1x+C_{2n}^2x^2-C_{2n}^3x^3+...-C_{2n}^{2n-1}x^{2n-1}+C_{2n}^{2n}x^{2n}\)
Thay \(x=1\) ta được:
\(0=C_{2n}^0-C_{2n}^1+C_{2n}^2-C_{2n}^3+..-C_{2n}^{2n-1}+C_{2n}^{2n}\)
\(\Leftrightarrow C_{2n}^0+C_{2n}^2+...+C_{2n}^{2n}=C_{2n}^1+C_{2n}^3+...+C_{2n}^{2n-1}\)
Đúng 1
Bình luận (0)
Rút gọn biểu thức:
P
2
n
+
4
-
2
(
2
n
)
2
(
2
n
+
3
)
. A.
2
n...
Đọc tiếp
Rút gọn biểu thức: P = 2 n + 4 - 2 ( 2 n ) 2 ( 2 n + 3 ) .
A. 2 n + 1
B. 1 - 2 n
C. 7 4
D. 7 8
rút gọn biểu thức a/b=(1/1*(2n-1)+1/3*(2n-3)+....+1/(2n-3)*3+1/(2n-1)*1)/1+1/3+1/5+...+1/2n-1
Mong các bạn giúp mình
\(A=\frac{1}{1\left(2n-1\right)}+\frac{1}{3\left(2n-3\right)}+...+\frac{1}{\left(2n-1\right).1}\)
\(A=\frac{1}{2n}\left[\frac{2n-1+1}{1\left(2n-1\right)}+\frac{2n-3+3}{3\left(2n-3\right)}+...+\frac{1+2n-1}{\left(2n-1\right).1}\right]\)
\(A=\frac{1}{2n}\left[\frac{1}{1}+\frac{1}{2n-1}+\frac{1}{3}+\frac{1}{2n-3}+...+\frac{1}{2n-1}+\frac{1}{1}\right]\)
\(A=\frac{1}{n}\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2n-3}+\frac{1}{2n-1}\right)\)
\(\Rightarrow\frac{a}{b}=\frac{1}{n}\).
Rút gọn biểu thúc
\(\frac{A}{B}=\frac{\frac{1}{1\left(2n-1\right)}+\frac{1}{3\left(2n-3\right)}+\frac{1}{5\left(2n-5\right)}+...+\frac{1}{\left(2n-3\right).3}+\frac{1}{\left(2n-1\right).1}}{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2n-1}}\)
\(\frac{1}{1.\left(2n-1\right)}+\frac{1}{3.\left(2n-3\right)}+...+\frac{1}{\left(2n-3\right).3}+\frac{1}{\left(2n-1\right).1}\)
\(=\frac{1}{2n}\left[\frac{2n-1+1}{1\left(2n-1\right)}+\frac{2n-3+3}{3\left(2n-3\right)}+...+\frac{3+2n-3}{\left(2n-3\right).3}+\frac{1+2n-1}{\left(2n-1\right).1}\right]\)
\(=\frac{1}{2n}\left(1+\frac{1}{2n-1}+\frac{1}{3}+\frac{1}{2n-3}+...+\frac{1}{2n-3}+\frac{1}{3}+\frac{1}{2n-1}+1\right)\)
\(=\frac{1}{n}\left(1+\frac{1}{3}+...+\frac{1}{2n-3}+\frac{1}{2n-1}\right)\)
\(\Rightarrow\frac{A}{B}=\frac{1}{n}\).
Rút gọn
\(\frac{A}{B}\)=\(\frac{\frac{1}{1\left(2n-1\right)}+\frac{1}{3\left(2n-3\right)}+\frac{1}{5\left(2n-5\right)}+...+\frac{1}{\left(2n-3\right)3}+\frac{1}{\left(2n-1\right)1}}{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2n-1}}\)
tìm số nguyên n để các phân số sau rút gọn được
3n2+2n+3
-------------
2n+1