xong het de chua

biết làm phần a câu 2 đề 13 ko

khong co stn abcd nao thoa man

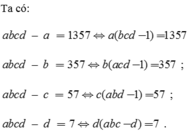
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức) 
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại 
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

Đáp án B

TH1: 4 chữ số a, b, c , d khác nhau →  có C 9 4  số

TH2: Trong 4 chữ số a, b, c , d có 3 chữ số giống nhau  →  có 3 C 9 3  số

TH3: Trong 4 chữ số a, b, c , d có 2 chữ số giống nhau  →  có 2 C 9 2  số

TH4: TH1: 4 chữ số a, b, c , d giống nhau  →  có C 9 1  số

Vậy có tất cả C 9 4 + 3 C 9 3 + 2 C 9 2 + C 9 1 = 459 số cần tìm

Đáp án B

TH1: 4 chữ số a, b, c , d khác nhau  → có C 9 4  số

TH2: Trong 4 chữ số a, b, c , d có 3 chữ số giống nhau → có 3 C 9 3  số

TH3: Trong 4 chữ số a, b, c , d có 2 chữ số giống nhau → có 2 C 9 1  số

TH4: TH1: 4 chữ số a, b, c , d giống nhau → có  C 9 1  số

Vậy có tất cả  C 9 4 + 3 C 9 3 + 2 C 9 1 + C 9 1 = 459  số cần tìm.

Đáp án:

Giải thích các bước giải:

 Không tồn tại số a,b,c,d 

Vì ta có  abcd  là số có 4 chữ số 

abcd-d=7 

 Số có 4 chữ số - số đơn vị=7( vô lí)

=> không tồn tại a,b,c,d

học tốt

vì abcd là sn có 4 c/s

=> abcd=a000+b00+c0+d

có abcd-d =abc0

=> chữ số cuối cùng của abcd phải là 0 mâu thuẫn với abcd-d=7

=> không tồn tại 4 chữ số nguyên a;b;c;d cần tìm

Ta có:

abcd chia hết cho 3 và 5 nên d phải là tận cùng bằng 5 hoặc 0

⇒a+b+c+d  phải chia hết cho 3

từ đó ta rút ra có 2 số chia hết cho 5 là 8765 và 3210 nhưng vì 8765 không chia hết cho 3 

⇒ số đó là 3210

Có  4 cách chia:

Cách chia bi nhiều túi nhất là cách 4,ta được 6 túi ,

Lần lượt chia đều bi đỏ vào 6 túi;

48:6= 8 (viên mỗi túi) 

Chia đều bi xanh vào 6 túi;

30 :6=5 (viên mỗi túi)

Chia đều bi vàng vào 6 túi;

66:6=11 (viên mỗi túi)

Tổng cộng số viên bi trong mỗi túi ;

8+5+11=24 (viên mỗi túi)