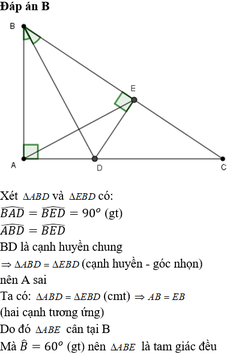
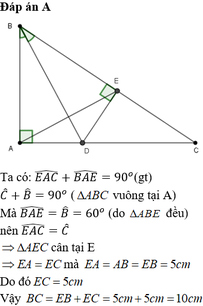
Cho tam giác ABC vuông tại A, góc B=60o ,AB=3cm.Tính AC,tan C

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, AD vuông góc BC , DE vuông góc AB , DF vuông góc AC
a, c/m tam giác DEF cân
b, c/m tam giác BDE =tam giác CDF
c, từ B kẻ đường thẳng // AD cắt AC tại M sao cho góc ABC = 30⁰ .c/m tam giác ABM đều
d, cho góc C =45⁰,AD=3cm.tính AC
giúp mình với mai mình phải nộp rồi
a)Ta thấy: tam giác ABC là tam giác cân, do AD vuông góc BC nên AD vừa là đường cao của tam giác đồng thời vừa là tia phân giác, đường trung tuyến của tam giác của tam giác ABC. Do D thuộc đường cao AD, mà DE và DF lần lượt thuộc hai cạnh bên của tam giác nên DE=DF. Từ đó suy ra tam giác DEF cân.
b) Xét tam giác BED vuông tại E và tam giác CDF vuông tại F ta có:
DB=DC(AD là đường trung tuyến của tam giác cân ABC)
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
Suy ra \(\Delta BED=\Delta CDF\)(cạnh huyền - góc nhọn)
c) Theo đề bài, \(\widehat{ABC}=30^o\)nên lúc này \(\widehat{ACB}=30^{^{ }o}\)
Cũng từ đó: \(\widehat{BAC}=180^o-30^{^{ }o}-30^{^{ }o}=120^o\)
Do \(\widehat{BAC}\)kề bù với \(\widehat{MAB}\)nên \(\widehat{MAB}=180^{o^{ }}-120^o=60^o\)(1)
Lại thấy: AD vuông góc với BC, MB//AD nên MB vuông góc BC. Suy ra \(\widehat{ABC}\)phụ \(\widehat{MBA}\)và \(\widehat{MBA}=90^o-30^o=60^o\)(2)
Từ (1) và (2), suy ra \(\widehat{AMB}=180^o-60^{o^{ }}-60^o=60^o\)và tam giác ABM đều.
Cho tam giac ABC vuông tại A .qua C vẽ tia Cx vuông góc với AC tại cắt đường cao AH của tam giác ABC tại M.chứng minh:
a,tam giác AHB đồng dạng với tam giác MHC.
b,chứng minh:CH2=AH.MH.
c,AH=2cm,CH=3cm.Tính AB,CM,S ABCM.
Cho tam giác ABC vuông tại A.Tia phân giác góc B cắt AC tại D.Biết góc C=30 độ,AC=3cm.Tính AD
Giải:
Hình bạn tự vẽ nhé.
Xét tam giác ABC vuông tại A có:
Góc C + góc ABC = 90o (định lí)
=> Góc ABC = 90o - góc C = 90o - 30o = 60o
=> Góc ABD = góc CBD = 60o : 2 = 30o
Xét tam giác ABD có:
Góc A = 90o (vì tam giác ABC vuông tại A) ; góc ABD = 30o (chứng minh trên)
=> AD = BD : 2 (định lí)
=> 2AD = BD (1)
Lại có: góc C = 30o (gt)
góc CBD = 30o (chứng minh trên)
=> Góc C = góc CBD
=> Tam giác BCD cân tại D (dấu hiệu nhận biết)
=> BD = CD (định lí) (2)
Từ (1), (2)
=> 2AD = CD
Mà AC = AD + CD
=> AD + 2AD = 3
=> 3AD = 3
=> AD = 1 (cm)
Vậy AD = 1cm.
Cho tam giác ABC vuông tại A.Tia phân giác góc B cắt AC tại D.Biết góc C bằng 30 độ,AC=3cm.Tính AD
Vì tam giác ABC vuông tại A có góc C = 30 độ
=> \(\hept{\begin{cases}AB=\frac{AC}{\sqrt{3}}=\frac{3}{\sqrt{3}}\left(cm\right)\\BC=\frac{2AC}{\sqrt{3}}=\frac{6}{\sqrt{3}}\left(cm\right)\end{cases}}\)
Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{AD}{DC}=\frac{AB}{BC}=\frac{\frac{3}{\sqrt{3}}}{\frac{6}{\sqrt{3}}}=\frac{1}{2}\Leftrightarrow\frac{DC}{AD}=2\)
\(\Leftrightarrow\frac{DC}{AD}+1=2+1\Leftrightarrow\frac{AC}{AD}=3\Rightarrow AD=\frac{AC}{3}=1\left(cm\right)\)
Vậy AD = 1 cm
Cho tam giác ABC vuông tại A, có
B
^
60
o
, AB5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại EChọn câu đúng A.
∆
A
B
D
∆
B
E
D
B.
∆
A
B
E
là tam giác đều C.
∆
A
B
E
là tam giác vuông cân D. Cả A,B,C đều sai
Đọc tiếp
Cho tam giác ABC vuông tại A, có B ^ = 60 o , AB=5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
Chọn câu đúng
A. ∆ A B D = ∆ B E D
B. ∆ A B E là tam giác đều
C. ∆ A B E là tam giác vuông cân
D. Cả A,B,C đều sai
cho tam giác abc vuông tại a đường cao ah
a,biết ah=6cm,bh=3cm.tính ab,ac
b,biết ab=6cm,bh=3cm.tính ah,ac,bh
a/
Xét tg vuông ABH
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+3^2}=3\sqrt{5}cm\)
\(AH^2=BH.CH\Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{6^2}{3}=12cm\)
Xét tg vuông ACH
\(AC=\sqrt{AH^2+CH^2}=\sqrt{6^2+12^2}=6\sqrt{5}cm\)
b/
\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}\)
CH=BC-BH
\(AH^2=BH.CH\)
Xét tg vuông ACH
\(AC=\sqrt{AH^2+CH^2}\)
Bạn tự thay số và tính toán nhé
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác trong của góc B cắt AC tại D
a. Cho BC = 10cm, AB = 6cm, AD = 3cm.Tính AC và CD
b. Vẽ DE vuông góc với BC tại E. CMR: tam giác ABD = tam giác EBD, và tam giác BAE cân
c Gọi F là giao điểm của hai đường thẳng AB và DE. So sánh DE và DF
A) XÉT \(\Delta ABC\)VUÔNG TẠI A
\(\Rightarrow BC^2=AB^2+AC^2\left(PYTAGO\right)\)
THAY \(10^2=6^2+AC^2\)
\(100=36+AC^2\)
\(\Rightarrow AC^2=100-36\)
\(\Rightarrow AC^2=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
ta có \(AD+DC=AC\)
\(\Leftrightarrow3+DC=8\)
\(\Leftrightarrow DC=8-3=5\left(cm\right)\)
B) XÉT \(\Delta ABD\)VÀ \(\Delta EBD\)CÓ
\(\widehat{BAD}=\widehat{BED}=90^o\)
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
BD LÀ CẠNH CHUNG
=>\(\Delta ABD\)=\(\Delta EBD\)( CH-GN)
\(\Rightarrow BA=BE\)(HAI CẠNH TƯƠNG ỨNG )
=> \(\Delta BAE\)LÀ TAM GIÁC CÂN TẠI B
c) XÉT \(\Delta ADF\)VUÔNG TẠI A
\(\Rightarrow DF>AD\left(1\right)\)( CẠNH HUYỀN LỚN NHẤT )
VÌ \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=> \(AD=ED\left(2\right)\)(HAI CẠNH TƯƠNG ỨNG )
TỪ (1) VÀ (2)
\(\Rightarrow DF>ED\)
Cho tam giác ABC vuông tại A, có B ^ = 60 o , AB=5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
Tính độ dài cạnh BC
A. 10cm
B. 5cm
C. 6cm
D. 8cm
Câu 6: Cho tam giác ABC vuông tại A, có B = 60o và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E.
a/ Chứng minh:tam giác ABD = tam giác EBD.
b/ Chứng minh: tam giácABE là tam giác đều.
c/ Tính độ dài cạnh BC.
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
Đúng 4
Bình luận (0)
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
\(\stackrel\frown{ABD}=\stackrel\frown{EBD}\)
\(BD\left(chung\right)\)
=> ΔABD=ΔEBD(c.h-gn)
:Ta có: ΔABD=ΔEBD(cmt)
nên BA=BE
=> ΔBAE cân tại B
mà \(\widehat{ABE}=60^o\)
=> ΔBAE đều(t/c tam giác cân)
Đúng 2
Bình luận (0)
TK
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
ˆABD=ˆEBDABD^=EBD^
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà ˆABE=600ABE^=600
nên ΔBAE đều
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A(AB<AC). Gọi M là trung điểm cạnh BC.Qua M vẽ MH vuông góc với AB tại H và MK vuông góc với AC tại K.
a, Biết AC=4cm, AB=3cm.Tính AM
b,tứ giác AKMH là hình gì?Tại sao?
c,Gọi N là điểm đối xứng của M qua H.Chứng minh AMBN là hình thoi