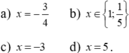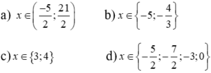giải phương trình : ( x2- 3x+2)(x2+15x+56)+8=0

Những câu hỏi liên quan
Giải phương trình sau đây :
a
)
8
(
3
x
-
2
)
-
14
x
2
(
4
–
7
x
)
+
15
x
b
)
(
3
x
–
1
)
(
x
–...
Đọc tiếp
Giải phương trình sau đây :
a ) 8 ( 3 x - 2 ) - 14 x = 2 ( 4 – 7 x ) + 15 x b ) ( 3 x – 1 ) ( x – 3 ) – 9 + x 2 = 0 c ) | x - 2 | = 2 x - 3 d ) x + 2 x - 2 - 1 x = 2 x x - 2
a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
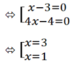
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
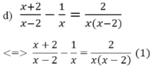
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2

Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1
Đúng 0
Bình luận (0)
a, Giải hệ phương trình:
3
x
-
2
y
+
1
1
5
x
+...
Đọc tiếp
a, Giải hệ phương trình: 3 x - 2 y + 1 = 1 5 x + 2 y + 1 = 3
b, Cho phương trình x 2 – (m – 1)x – m 2 – 1 = 0 với x là ẩn và m là tham số. Tìm m để phương trình có hai nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 2 2
a, Cách 1. Đặt 1 y + 1 = u ta được 3 x - 2 u = 1 5 x + 2 u = 3
Giải ra ta được x = 1 2 ; u = 1 4
Từ đó tìm được y = 3
Cách 2. Cộng vế với vế hai phương trình, ta được 8x = 4
Từ đó tìm được x = 1 2 và y = 3
b, Vì x1x2 = -m2 - 1 < 0 "m nên phương trình đã cho luôn có hai nghiệm phân biệt và trái dấu.
Cách 1. Giả sử x 1 < 0 < x 2
Từ giả thiết thu được – x 1 + x 2 = 2 2
Biến đổi thành x 1 + x 2 2 - 4 x 1 x 2 = 8
Áp dụng định lý Vi-ét, tìm được m = 1 hoặc m = - 3 5
Cách 2. Bình phương hai vế của giả thiết và biến đổi về dạng
x 1 + x 2 2 - 2 x 1 x 2 + 2 x 1 x 2 = 8
=> m - 1 2 + 4 m 2 + 1 = 8
Do x 1 x 2 = - x 1 x 2
Áp dụng hệ thức Vi-ét, ta cũng tìm được m = 1 hoặc m = - 3 5
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
2
x
+
4
1
−
2
x
;
b)
15
x
−
7
−
5
x
+
3
0
;
c)...
Đọc tiếp
Giải các phương trình sau:
a) 2 x + 4 = 1 − 2 x ; b) 15 x − 7 − 5 x + 3 = 0 ;
c) x 2 − 9 + 3 x + 3 = 0 ; d) 3 1 3 x − 2 = 4 1 − x 4
Giải các phương trình sau bằng cách đặt ẩn số phụ x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0
Đặt m = x 2 +3x -1
Ta có: x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0 ⇔ m 2 +2m -8 =0
∆ ’ = 1 2 -1.(-8) =1 +8 =9 > 0
∆ ' = 9 =3
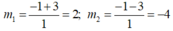
Với m = 2 thì : x 2 +3x - 1 = 2 ⇔ x 2 + 3x - 3 = 0
∆ ’ = 3 2 -4.1.(-3 )=9 +12=21 > 0
∆ ' = 21
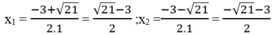
Với m = -4 ta có: x 2 +3x -1 = -4 ⇔ x 2 +3x +3 = 0
∆ = 3 2 -4.1.3=9 -12 = -3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
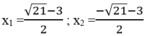
Đúng 0
Bình luận (0)
Hãy giải các phương trình sau đây :
1, x2 - 4x + 4 = 0
2, 2x - y = 5
3, x + 5y = - 3
4, x2 - 2x - 8 = 0
5, 6x2 - 5x - 6 = 0
6,( x2 - 2x )2 - 6 (x2 - 2x ) + 5 = 0
7, x2 - 20x + 96 = 0
8, 2x - y = 3
9, 3x + 2y = 8
10, 2x2 + 5x - 3 = 0
11, 3x - 6 = 0
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
Đúng 1
Bình luận (0)
giải phương trình
\(\left(x^2-3x+2\right)\left(x^2+15x+56\right)+8\)\(=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+7\right)\left(x+8\right)+8=0.\)
\(\Leftrightarrow\left(x-1\right)\left(x+7\right)\left(x-2\right)\left(x+8\right)+8=0.\)
\(\Leftrightarrow\left(x^2+6x-7\right)\left(x^2+6x-16\right)+8=0.\)
đặt \(\left(x^2+6x-7\right)=a.\)
\(a\left(a-9\right)+8=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=1\\a=8\end{cases}}\)
thay ròi giả tiếp .
Đúng 0
Bình luận (0)
(x^2-x-2x+2)(x^2+8x+7x+56)+8=0
{x(x-1)-2(x-1)}{x(x+8)+7(x+8)}+8=0
(x-1)(x-2)(x+8)(x+7)+8=0
(x-1)(x-2)(x+8)(x+7)=-8
Đúng 0
Bình luận (0)
jjjgjjjvjvjijmkjiuenndmddnđndndndndnndndndnndndnndnndnd
Xem thêm câu trả lời
giải phương trình:(x2-3x)2+5(x2-3x)+6=0
Đặt x2 - 3x = t
phương trình trở thành: t2 + 5t + 6 = 0
=> t2 + 3t + 2t + 6 = 0
=> t(t+3) + 2(t+3) = 0
=> (t+3)(t+2) = 0
=> \(\left[{}\begin{matrix}t+2=0\\t+3=0\end{matrix}\right.\)
Thay lại t = x2 - 3x vào hai trường hợp trên, giải phương trình ta được:
+ TH1: t+2 = 0 => x = 1 hoặc x = 2.
+ TH2: t+3 = 0 => vô nghiệm
Vậy, giá trị của x thỏa mãn phương trình là 1 hoặc 2.
Đúng 1
Bình luận (0)
Giải các phương trình sau:a)
2
x
+
5
6
−
1
3
2
x
+
5
x
−
10
0
;
b)
4
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 2 x + 5 6 − 1 3 2 x + 5 x − 10 = 0 ;
b) 4 x − 1 x + 5 = x 2 − 25 ;
c) 3 x − 3 2 − x − 3 x + 2 4 = 0 ;
d) x x + 3 3 − x 4 x + 3 = 0 .
Giải các hệ phương trình sau bằng phương pháp thế:
a
)
3
x
−
2
y
11
4
x
−...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp thế:
a ) 3 x − 2 y = 11 4 x − 5 y = 3 b ) x 2 − y 3 = 1 5 x − 8 y = 3
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
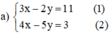
Từ (1) ta rút ra được y = 3 2 x − 11 2 (*)
Thế (*) vào phương trình (2) ta được :
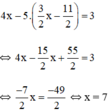
Thay x = 7 vào (*) ta suy ra y = 3 2 ⋅ 7 − 11 2 = 5
Vậy hệ phương trình có nghiệm duy nhất (7 ; 5).
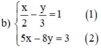
Từ (1) ta rút ra được : y = 3 2 x − 3 (*)
Thế (*) vào phương trình (2) ta được :
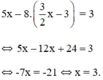
Thay x = 3 vào (*) ta suy ra
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Cách 2:
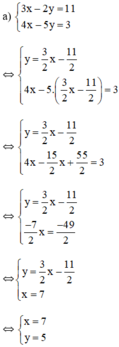
Vậy hệ phương trình có nghiệm duy nhất (7; 5).
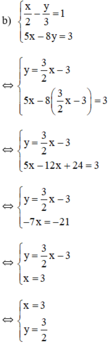
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Kiến thức áp dụng
Giải hệ phương trình 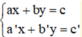 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
Đúng 0
Bình luận (0)