Vì xOy và xOy' là 2 góc kề bù

=> xOy + xOy' = 180*

Thay xOy = 60*

=> xOy' = 180* - 60*

xOy' = 120*

Vì xx' và yy' cắt nhau tại O

=> xOy và x'Oy' là 2 góc đối đỉnh mà xOy = 60*

=> xOy = x'Oy' = 60*

Vì x'Oy là góc đối đỉnh của xOy' mà xOy' = 120*

=> x'Oy = 120*

Tính rõ rồi nha bạn, nếu cần chứng minh 2 góc đối đỉnh, lm đầy đủ hơn nữa thì bảo mik, cn như này là cx đc điểm tối đa òi

Ta có:

Do \(\widehat{xOy}\) và \(\widehat{xOy'}\) là 2 góc kề bù

\(\Rightarrow\)\(\widehat{xOy}\) + \(\widehat{xOy'}\) = 180^o 

\(\Rightarrow\)60^o + \(\widehat{xOy'}\) = 180^o

\(\Rightarrow\)\(\widehat{xOy'}\) = 180^o - 60^o = 120^o

Vậy  \(\widehat{xOy'}\)= 120^o

 Ta có:

Do \(\widehat{xOy}\)và góc \(\widehat{x'Oy'}\) là 2 góc đối đỉnh

\(\Rightarrow\)\(\widehat{xOy}=\widehat{x'Oy'}=60^o\)

Ta có:

Do \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là 2 góc kề bù

\(\Rightarrow\widehat{xOy}+\widehat{x'Oy}=180^o\)

\(\Rightarrow60^o+\widehat{x'Oy}=180^o\)

\(\Rightarrow\widehat{x'Oy}=180^o-60^o=120^o\)

Vậy \(\widehat{x'Oy=120^o}\)

 Hoặc bạn có thể giải bằng cách này thì ngắn gọn hơn

Ta có:

Do \(\widehat{xOy'}\) và \(\widehat{x'Oy}\) là hai góc đối đỉnh

\(\Rightarrow\widehat{xOy'}=\widehat{x'Oy}=120^o\)

Vậy \(\widehat{x'Oy}=120^o\)

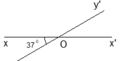
x ' O y ' ^ = 30 ° ,     x ' O y ^ = 150 ° ,    x O y ' ^ = 150 ° .

\(\widehat{xOy}+\widehat{x'Oy=180^0}\)  (Vì \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là hai góc kề bù)

\(\widehat{xOy}-\widehat{x'Oy}=40^0\)

a.\(\widehat{xOy}=\left(180^0+40^0\right):2=110^0\)

\(\widehat{x'Oy'}=\widehat{xOy}=110^0\) ( 2 góc đối đỉnh)

b. \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-110^0=70^0\) (2 góc kề bù)

\(\widehat{xOy'}=\widehat{x'Oy}=70^0\) ( 2 góc đối đỉnh)

\(\widehat{xOy}=\widehat{x'Oy'}=120^0;\widehat{x'Oy}=\widehat{xOy'}=60^0\)

ta có: góc xOy' + góc x'Oy' = 180 độ ( kề bù)

=> 4.góc x'Oy' + góc x'Oy' = 180 độ

5.góc x'Oy' = 180 độ

góc x'Oy' = 180 độ : 5

góc x'Oy' = 36 độ

=> góc x'Oy' = góc xOy = 36 độ ( đối đỉnh)

=> góc xOy = 36 độ

mà góc xOy + góc x'Oy = 180 độ ( kề bù)

thay số: 36 độ + góc x'Oy = 180 độ

góc x'Oy = 180 độ - 36 độ

góc x'Oy = 144 độ

=> góc x'Oy = góc xOy' = 144 độ ( đối đỉnh)

=> góc xOy' = 144 độ

tự kẻ hình nha bn

Ta có : xOy' + x'Oy' =180⁰

xOy' = 4x'Oy'

=> xOy' = 36⁰

     x'Oy' = 144⁰

=> xOy' = x'Oy = 36⁰

     x'Oy' = xOy = 144⁰

Giải
_  Ta có  \(\widehat{xOy}=\widehat{x'Oy'}=40^0\)( đối đỉnh) => \(\widehat{xOm}=\widehat{mOy}=\widehat{y'On}=\widehat{nOx'}=\frac{40^0}{2}=20^0\)
_  \(\widehat{x'Oy}=\widehat{xOy'}=180^0-40^0=140^0\)

ghjhhhfghdfhgd