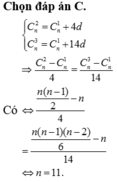số nguyên dương n lớn nhất thỏa mãn : n^200<5^300

Những câu hỏi liên quan
Tính số nguyên n lớn nhất thỏa mãn n 200 < 5 300 .
A. 10
B. 11
C. 12
D. 13
Tính số nguyên n lớn nhất thỏa mãn n 200 < 5 300 .
A. 10
B. 11
C. 12
D. 13
số nguyên dương n lớn nhất thoả mãn n200<5300
\(n^{200}<5^{300}=>\left(n^2\right)^{100}<\left(5^3\right)^{100}=>n^2<5^3=125=>n^2\in\left\{0;4;9;...;121\right\}\)
mà n lớn nhất nên n^2=121=>n=11
tick nhé
Đúng 0
Bình luận (0)
Tìm số nguyên dương n lớn nhất để tồn tại đúng một số nguyên dương k thoả mãn \(\frac{8}{21}< \frac{n}{n+k}< \frac{5}{13}\)
Tìm số nguyên dương n lớn nhất để tồn tại đúng một số nguyên dương k thoả mãn
\(\frac{8}{21}< \frac{n}{n+k}< \frac{5}{13}\)
Cho hai số m và n nguyên dương và nguyên tố cùng nhau thoả mãn m+n=90. Tìm giá trị lớn nhất của m nhân n .
các bạn giúp mình với nhé
Lời giải:
Vì $m,n$ nguyên tố cùng nhau, $m+n=90$ chẵn nên $m,n$ là hai số lẻ phân biệt.
Không mất tổng quát giả sử $m>n$.
$90=m+n>2n\Rightarrow n< 45$. Vì $n$ lẻ nên $n\leq 43$.
Có:
$mn=(90-n)n=90n-n^2=n(43-n)-47(43-n)+43.47$
$=(n-47)(43-n)+2021$
Vì $n\leq 43$ nên $n-47< 0; 43-n\geq 0\Rightarrow (n-47)(43-n)\leq 0$
$\Rightarrow mn\leq 2021$. Giá trị này đạt tại $n=43, m=47$ thỏa mãn điều kiện đề.
Vậy GTLN của $mn$ là $2021$.
Đúng 0
Bình luận (0)
tìm các số nguyên dương m,n với m lớn nhất và thoả mãn \(5m^2-12mn+12n^2+4m=1648\)
Xét dãy
u
n
:
u
n
n
+
1
n
khi đó số α dương lớn nhất thoả mãn
u
n
≥
α
∀
n
≥
1
là: A. α1 B. α2 C. α1/2 D.
α
2
Đọc tiếp
Xét dãy u n : u n = n + 1 n
khi đó số α dương lớn nhất thoả mãn u n ≥ α ∀ n ≥ 1 là:
A. α=1
B. α=2
C. α=1/2
D. α = 2
cho các số nguyên dương a,b,c,d thoả mãn a+b=c+d=1000 hỏi khi nào tổng a/c+b/d đạt giá trị lớn nhất
Cho số nguyên dương n thoả mãn
C
n
1
;
C
n
2
;
C
n
3
lần lượt là số hạng thứ nhất, thứ 5 và thứ 15 của một cấp số cộng. Giá trị của n bằng
Đọc tiếp
Cho số nguyên dương n thoả mãn C n 1 ; C n 2 ; C n 3 lần lượt là số hạng thứ nhất, thứ 5 và thứ 15 của một cấp số cộng. Giá trị của n bằng
![]()
![]()
![]()
![]()