trong mặt phảng toạn độ Oxy, cho tam giác ABC có phương trình các cạnh AB, AC lần lượt là x=0; x-y=0. phép vị tự tâm 0 tỉ số k= -3 biến tam giác A'B'C'. khi đó góc A' của tam giác A'B'C' có số đo là?

Những câu hỏi liên quan
trong mặt phẳng hệ tọa độ Oxy cho tam giác ABC cân tại A . biết phương trình các đường thẳng AB,BC lần lượt là x-7y+14=0 và 2x+y-2=0. viết phương trình cạnh AC , biết đường thẳng AC đi qua M(4,0)
\(cosB=\dfrac{\left|1.2+\left(-7\right).1\right|}{\sqrt{1^2+\left(-7\right)^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)
Gọi vtpt của AC có tọa độ \(\left(a;b\right)\)
\(\Rightarrow cosC=cosB=\dfrac{1}{\sqrt{10}}=\dfrac{\left|2a+b\right|}{\sqrt{a^2+b^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow2\left(2a+b\right)^2=a^2+b^2\)
\(\Leftrightarrow7a^2+8ab+b^2=0\Leftrightarrow\left(a+b\right)\left(7a+b\right)=0\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}b=-1\\b=-7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;-7\right)\end{matrix}\right.\)
(Trường hợp \(\left(a;b\right)=\left(1-;7\right)\) loại do khi đó AC song song AB, vô lý)
\(\Rightarrow\) Phương trình AC: \(1\left(x-4\right)-1\left(y-0\right)=0\)
Đúng 2
Bình luận (1)
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
Chọn A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
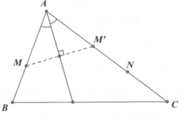
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.



Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M(2;0) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x-2y-3=0 và 6x-y-4=0. Phương trình đường thẳng AC là:
A.3x-4y-5=0
B.3x+4y+5=0
C.3x-4y+5=0
D.3x+4y-5=0
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
M
(
2
;
0
)
là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là
7
x
-
2
y
-
3
0
và
6
x
-
y
-
4
0
. Phương trình đường thẳng AC...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm
M
4
;
-
1
,
N
0
;
-
5
lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là
x
-
3
y
+
5
0
, trọng tâm của tam giác ABC là G. Tìm toạ...
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M 4 ; - 1 , N 0 ; - 5 lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x - 3 y + 5 = 0 , trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC
A. A 1 ; 2 , B - 2 ; 5 , C - 1 ; 12
B. A 1 ; 2 , B - 2 ; 5 , C 0 ; 1
C. A 1 ; 0 , B - 2 ; 5 , C - 1 ; 12
D. A 1 ; 2 , B - 1 ; 5 , C - 1 ; 12
Đáp án A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
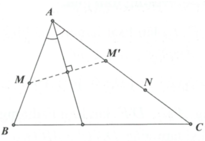
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
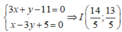
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
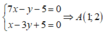
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
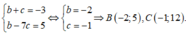
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()
Đúng 0
Bình luận (0)
1. Trong mặt phẳng Oxy cho tam giác ABC có trọng tâm G(−2; 0) biết phương trình các cạnh AB, AC theo thứ tự là 4x+y+14=0; 2x+5y-2=0. Tìm tọa độ các đỉnh A, B, C.
2.Lập phương trình các cạnh AB, AC của tam giác ABC biết đường tuyến CM có phương trình 2x+y-6=0, A(1; 1) và cạnh BC có phương trình x+y-6=0
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x - y + 1 0 và x + y - 4 0. Phương trình đường thẳng AD là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x - y + 1 = 0 và x + y - 4 = 0. Phương trình đường thẳng AD là
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2xy+10 và x+y-40 Phương trình đường thẳng AD là A. x+2y+50 B. x-2y+50 C. x+2y-70 D. x-2y-70
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x=y+1=0 và x+y-4=0 Phương trình đường thẳng AD là
A. x+2y+5=0
B. x-2y+5=0
C. x+2y-7=0
D. x-2y-7=0
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x - y + 1 0 và x + y -4 0. Phương trình đường thẳng AD là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là
2x - y + 1 = 0 và x + y -4 = 0. Phương trình đường thẳng AD là
![]()
![]()
![]()
![]()















