Tìm m để đồ thị hàm số sau nhận trục tung làm tâm đối xứng y = ( m2 - 3m + 2).x3 + m2 - 1
Mọi người giúp em với ạ (>w<)
Những câu hỏi liên quan
Tìm m để đồ thị hàm số sau nhận gốc toạ độ O làm tâm đối xứng :
\(y=x^3-\left(m^2-9\right)x^2+\left(m+3\right)x+m-3\)
https://vungoi.vn/cau-hoi-39983
Ta có TXĐ:D=R
⇒∀x∈D⇒−x∈D
Đồ thị hàm số đã cho nhận gốc tọa độ O làm tâm đối xứng khi và chỉ khi nó là hàm số lẻ
⇔f(−x)=−f(x),∀x∈R
\(\text{⇔(−x)^3−(m^2−9)(−x)^2+(m+3)(−x)+m−3}\)
\(\text{=-[x^3−(m^2−9)x^2+(m+3)x+m−3]}\)
\(=\text{⇔2(m^2−9)x^2−2(m−3)=0}\)
\(\Rightarrow\forall\inℝ\) ;
\(\hept{\begin{cases}m^2-9=0\\m-3=0\end{cases}}\)
\(\hept{\begin{cases}m=\pm3\\m=3\end{cases}}\)
\(\Rightarrow m=3\)
Tìm m để hàm số
y
-
x
3
+
(
2
m
+
1
)
x
2
-
(
m
2
-
3
m
+
2
)
x
-
4
có cực đại, cực tiểu nằm về hai phía so với trục tung A. m ∈ (1; 2) B. m ∈ [1; 2] C. m ∈ (- ∞; 1) ∪ (2; +∞) D. m ∈ (- ∞; 1] ∪ [2; +∞)
Đọc tiếp
Tìm m để hàm số y = - x 3 + ( 2 m + 1 ) x 2 - ( m 2 - 3 m + 2 ) x - 4 có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2)
B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞)
D. m ∈ (- ∞; 1] ∪ [2; +∞)
y ' = - 3 x 2 + 2 ( 2 m + 1 ) x - m 2 + 3 m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x 1 , x 2 trái dấu.
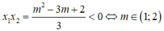
Chọn A
Đúng 0
Bình luận (0)
Cho hàm số: y(m-1)x+m (d)a, Tìm m để hàm số đồng biến, nghịch biếnb, Tìm m để hàm số song song với trục hoànhc, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y1e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ x2-frac{sqrt{3}}{2}f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Đọc tiếp
Cho hàm số: y=(m-1)x+m (d)
a, Tìm m để hàm số đồng biến, nghịch biến
b, Tìm m để hàm số song song với trục hoành
c, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)
d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y=1
e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ \(x=2-\frac{\sqrt{3}}{2}\)
f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Cho hàm số: y = mx + m - 1 (m khác 0) có đồ thì cắt 2 trục tọa tại A, B. Tìm m để diện tích tam giác AOB là 2
Mn giúp mk với ạ...
Hệ số góc của tiếp tuyến của đồ thị hàm số y = x - 1 x + 1 tại giao điểm của đồ thị hàm số với trục tung bằng
A. -2
B. 2
C. -1
D. 1
Giao điểm với trục tung B(0 ;-1). Ta có
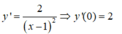
Hệ số góc của tiếp tuyến của đồ thị hàm số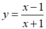 
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
2
-
m
(m là tham số) có đồ thị
C
m
. Tập hợp các giá trị của tham số m để đồ thị
C
m
cắt trục hoành tại ba điểm phân biệt là tập hợp nào sau đây? A.
A
-...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 - m (m là tham số) có đồ thị C m . Tập hợp các giá trị của tham số m để đồ thị C m cắt trục hoành tại ba điểm phân biệt là tập hợp nào sau đây?
A. A = - 4 ; 0
B. A = - ∞ ; - 4 ∪ 0 ; + ∞
C. A = ℝ
D. A = - 4 ; 0
Cho hàm số: y= x^2/4
a/ Vẽ đồ thị hàm số (P)
b/ Tìm các điểm M thuộc đồ thị hàm số (P) sao cho hoành độ và tung độ là hai số đối nhau.
Phương trình tiếp tuyến với đồ thị
C
1
của hàm số
y
x
3
-
1
tại giao điểm của đồ thị
C
1
vớitrục hoành có phương trình A.
y
3
x
-
1
B.
y
3
x
-
3
C....
Đọc tiếp
Phương trình tiếp tuyến với đồ thị C 1 của hàm số y = x 3 - 1 tại giao điểm của đồ thị C 1 với
trục hoành có phương trình
A. y = 3 x - 1
B. y = 3 x - 3
C. y = 0
D. y = 3 x - 4
Số giao điểm của đồ thị hàm số y = x 3 - 3 x 2 + 2 x + 1 với trục hoành là
A. 0
B. 1
C. 2
D. 4
