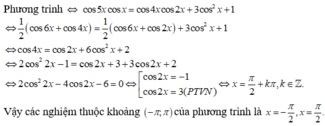Phương trình cos5x.cosx = cos4x.cos2x + 3cos^2x - 1 có các nghiệm thuộc (-pi: pi) là

Những câu hỏi liên quan
Phương trình cos5x.cosx = cos4x.cos2x + 3cos^2x - 1 có các nghiệm thuộc (-pi: pi) là
\(\Leftrightarrow\frac{1}{2}cos6x+\frac{1}{2}cos4x=\frac{1}{2}cos6x+\frac{1}{2}cos2x+3cos^2x-1\)
\(\Leftrightarrow cos4x-cos2x-6cos^2x+2=0\)
\(\Leftrightarrow2cos^22x-1-cos2x-3\left(cos2x+1\right)+2=0\)
\(\Leftrightarrow2cos^22x-4cos2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=1+\sqrt{2}>1\left(l\right)\\cos2x=1-\sqrt{2}\end{matrix}\right.\)
Bạn coi lại đề, nghiệm xấu quá, biện luận thì cũng được thôi nhưng chắc chẳng ai cho đề như vầy bao giờ cả
Đúng 0
Bình luận (0)
Cho phương trình cos5x.cosx cos4x.cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là: A. B. C. D.
Đọc tiếp
Cho phương trình cos5x.cosx = cos4x.cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
1) tìm m để phương trình 2sinx+mcosx1-m có nghiệm x thuộc left[-frac{pi}{2};frac{pi}{2}right]
2) tìm nghiệm của phương trình : sinx^24x+3.sin4x.cos4x-4.cos^24x0 khoảng left(0;frac{pi}{2}right)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx cos4x.cos2x+ 3cos^2x+1 thuộc khoảng left(-pi;piright)
4) tìm tất cả các nghiệm trong khoảng (frac{2pi}{5};frac{6pi}{7}) của phương trình: sqrt{3}sin7x-cos7xsqrt{2}
Đọc tiếp
1) tìm m để phương trình 2sinx+mcosx=1-m có nghiệm x thuộc \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
2) tìm nghiệm của phương trình : \(sinx^24x+3.sin4x.cos4x-4.cos^24x=0\) khoảng \(\left(0;\frac{\pi}{2}\right)\)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx= cos4x.cos2x+ \(3cos^2x+1\) thuộc khoảng \(\left(-\pi;\pi\right)\)
4) tìm tất cả các nghiệm trong khoảng (\(\frac{2\pi}{5};\frac{6\pi}{7}\)) của phương trình: \(\sqrt{3}sin7x-cos7x=\sqrt{2}\)
1:cho phương trình sau: \(sinx+\frac{sinx+cos3x}{1+2sinx}=\frac{3+cos2x}{5}\).
tìm các nghiệm thuộc khoảng từ \(\left(0,2\pi\right)\)
2:cho phương trình sau: \(cos5x.cosx=cos4x.cos2x+3cos2x+1\).
tìm các nghiệm thuộc khoảng từ \(\left(-\pi;\pi\right)\)
a) cos5x.cosx= cos4x.cos2x+3cos^2x+1
b)cos7x - sin2x-1=0
Câu 1: Phương trình lượng giác: sin^2 x - 3cos x - 4 = 0 có nghiệm là: A. x=- pi 2 +k 2 pi B. x=- pi+k2 pi C. x = pi/6 + k*pi D.Vô nghiệm
1.D
sin2x - 3cosx - 4 = 0
1-cos2x - 3cosx - 4 = 0
cos2x + 3 cosx + 3 = 0
Vô nghiệm
Đúng 0
Bình luận (0)
Cho phương trình (1-Sinx)(Cos2x + 3mSinx+Sinx-1)=\(mCos^2x\) (m là tham số). Tìm các giá trị thực của m để phương trình có 6 nghiệm khác nhau thuộc khoảng \(\left(-\dfrac{\Pi}{2};2\Pi\right)\)
\(\Leftrightarrow\left(1-sinx\right)\left(cos2x+3msinx+sinx-1\right)=m\left(1-sinx\right)\left(1+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}\\cos2x+3m.sinx+sinx-1=m\left(1+sinx\right)\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 5 nghiệm khác nhau trên khoảng đã cho thỏa mãn \(sinx\ne1\)
Xét (1):
\(\Leftrightarrow1-2sin^2x+3msinx+sinx-1=m+m.sinx\)
\(\Leftrightarrow2sin^2x-sinx-2m.sinx+m=0\)
\(\Leftrightarrow sinx\left(2sinx-1\right)-m\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{6};\dfrac{5\pi}{6}\\sinx=m\left(2\right)\end{matrix}\right.\)
\(\Rightarrow\left(2\right)\) có 3 nghiệm khác nhau trên \(\left(-\dfrac{\pi}{2};2\pi\right)\)
\(\Leftrightarrow-1< m< 0\)
Đúng 0
Bình luận (1)
1. Tập hợp tất cả các nghiệm thuộc [-pi;pi] của pt 2sin^2x + 2sin2x=3-3cos^2x là
2. Phương trình 2cos^x-3√3sin2x-4sin^2=-4 có số nghiệm thuộc (0;2pi) là ?
Giúp mik/em với ạ
1.
\(2sin^2x+4sinx.cosx=3-3cos^2x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(\Rightarrow2tan^2x+4tanx=3\left(1+tan^2x\right)-3\)
\(\Leftrightarrow2tan^2x+4tanx=3tan^2x\)
\(\Leftrightarrow tan^2x-4tanx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=arctan\left(4\right)+k\pi\end{matrix}\right.\)
Các nghiệm thỏa mãn là: \(\left\{-\pi;0;\pi;arctan\left(4\right)-\pi;arctan\left(4\right)\right\}\)
Có 5 nghiệm trên đoạn đã cho
Đúng 0
Bình luận (0)
2.
Chắc đề là \(2cos^2x-3\sqrt{3}sin2x-4sin^2x=-4\)
\(\Leftrightarrow2cos^2x-6\sqrt{3}sinx.cosx+4\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2cos^2x-6\sqrt{3}sinx.cosx+4cos^2x=0\)
\(\Leftrightarrow6cos^2x-6\sqrt{3}sinx.cosx=0\)
\(\Leftrightarrow6cosx\left(cosx-\sqrt{3}sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\tanx=\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{6}+k\pi\end{matrix}\right.\)
Các nghiệm thuộc đoạn đã cho: \(\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{\pi}{6};\frac{7\pi}{6}\right\}\) có 4 nghiệm thỏa mãn
Đúng 0
Bình luận (0)
Cho phương trình \(\left(cosx+1\right)\left(4cos2x-mcosx\right)=msin^2x\) . Số các giá trị nguyên của m để phương trình có đúng 2 nghiệm thuộc \(\left[0;\dfrac{2\pi}{3}\right]\) là
\(\Leftrightarrow\left(cosx+1\right)\left(4cos2x-m.cosx\right)=m\left(1-cosx\right)\left(1+cosx\right)\)
\(\Leftrightarrow4cos2x-m.cosx=m\left(1-cosx\right)\)
\(\Leftrightarrow4cos2x=m\)
\(\Rightarrow cos2x=\dfrac{m}{4}\)
Pt có đúng 2 nghiệm thuộc đoạn đã cho khi và chỉ khi:
\(-1< \dfrac{m}{4}\le-\dfrac{1}{2}\Leftrightarrow-4< m\le-2\)
Có 2 giá trị nguyên của m thỏa mãn
Đúng 0
Bình luận (0)