Cho tam giác ABC có AB = AC, I là trung điểm của BC. Trên tia AI kéo dài
lấy điểm E sao cho IE = IA.
a) Chứng minh: ΔAIB = ΔAIC. b) Chứng minh: AB // EC.
c) Từ A vẽ đường thẳng vuông góc với AB cắt BC tại D. Chứng minh EC AD
.

Những câu hỏi liên quan
Cho tam giác ABC có AB = AC, I là trung điểm của BC. Trên tia AI kéo dài
lấy điểm E sao cho IE = IA.
a) Chứng minh: ΔAIB = ΔAIC. b) Chứng minh: AB // EC.
c) Từ A vẽ đường thẳng vuông góc với AB cắt BC tại D. Chứng minh EC AD
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm
a. Tính độ dài BC
b. So sánh các góc của tam giác ABC
c. Vẽ đường phân giác BD của tam giác ABC (D thuộc AC). Vẽ DB vuông góc với BC tại E. Chứng minh tam giác ABD = tam giác EBD
d. Trên tia đối của tia AB, lấy điểm K sao cho AK = EC
Chứng minh góc BKC bằng góc BCK
e. Tia BD cắt KC tại I. Chứng minh IA = IE.
Cho tam giác ABC, lấy điểm I là trung điểm của cạnh BC. Trên tia đối của tia IA lấy điểm E sao cho IE = IA. a)Chứng minh tam giác AIB = tam giác AIC.
b)Chứng minh AI vuông góc với BC
c)Chứng minh AB//EC
a: Xét ΔAIB và ΔAIC có
AB=AC
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: Xét tứ giác ABEC có
I là trung điểm của AE
I là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
Đúng 1
Bình luận (0)
Cho ∆ ABC ( AB<AC), I là trung điểm của BC
Trên tia đối của IA lấy điểm E sao cho IE=IA
a) Chứng minh: ∆AIB=∆EIC
b) Chứng minh: AB=EC
c) Kẻ đường thẳng d và vuông góc với AB. Chứng minh: d vuông góc với CE
a/ \(\Delta AIB\)và \(\Delta EIC\)có: IB = IC (I là trung điểm của BC)
\(\widehat{AIB}=\widehat{EIC}\)(đối đỉnh)
AI = EI (gt)
=> \(\Delta AIB=\Delta EIC\)(c. g. c) (đpcm)
b) Ta có: \(\Delta AIB=\Delta EIC\)(cmt) => AB = EC (hai cạnh tương ứng) (đpcm)
c) Ta có: \(\Delta AIB=\Delta EIC\)(cm câu a) => \(\widehat{B}=\widehat{C}\)(hai góc tương ứng bằng nhau ở vị trí so le trong) => AB // EC
Mà AB _|_ d => EC _|_ d (đpcm)
Đúng 0
Bình luận (0)
Bài 1: Cho góc xOy 90 độ có tia phân giác Ot. Từ điểm A thuộc tia Ot vẽ AB vuông góc với Ox ( B thuộc Ox)a) Chứng minh AB song song với Oyb) Tính số đo góc OABBài 2: Cho tam giác ABC có AB AC. Gọi H là trung điểm của BC. Qua B vẽ đường thẳng song song với AH, đường thẳng này cắt đường thẳng AC tại Da) Chứng minh: tam giác AHB TAM GIÁC AHCb) Chứng minh AH vuông góc với BC và góc CBD 90 độc) Vẽ AI vuông góc svoiws BD( I thuộc BD). Chứng minh IB IDBài 3: Cho tam giác ABC vuông tại A,M là trung...
Đọc tiếp
Bài 1: Cho góc xOy = 90 độ có tia phân giác Ot. Từ điểm A thuộc tia Ot vẽ AB vuông góc với Ox ( B thuộc Ox)
a) Chứng minh AB song song với Oy
b) Tính số đo góc OAB
Bài 2: Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC. Qua B vẽ đường thẳng song song với AH, đường thẳng này cắt đường thẳng AC tại D
a) Chứng minh: tam giác AHB = TAM GIÁC AHC
b) Chứng minh AH vuông góc với BC và góc CBD = 90 độ
c) Vẽ AI vuông góc svoiws BD( I thuộc BD). Chứng minh IB= ID
Bài 3: Cho tam giác ABC vuông tại A,M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AB // CE
b) BE vuông góc với EC
c) AM = 1/2 BC
Cho tam giác ABC vuông tại A có AB AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB ACG
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de = AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE = AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB = ACG
Cho tam giác ABC vuông tại A có AB=3cm, AC=4cm
a) Tính độ dài BC
b) Vẽ đường phân giác BD của tam giác ABC (D thuộc AC). Vẽ DE vuông BC tại E. Chứng minh: tam giác ABD= tam giác EBD
c) Trên tia đối của tia AB lấy điểm K sao cho AK=EC. Chứng minh: góc BKC= góc BCK
d) Tia BD cắt KC tại I. Chứng minh: IA=IE
cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC. a) chứng minh tam giác AIB = tam giác AIC b) Kẻ đường thẳng qua I và vuông góc với AB tại D. Trên tia đối của tia ID lấy điểm E sao cho ID = IE. Chứng minh AB // CE c) Kẻ EK vuông góc với BC tại K, cắt cạnh AC tại H. Chứng minh HD // AI
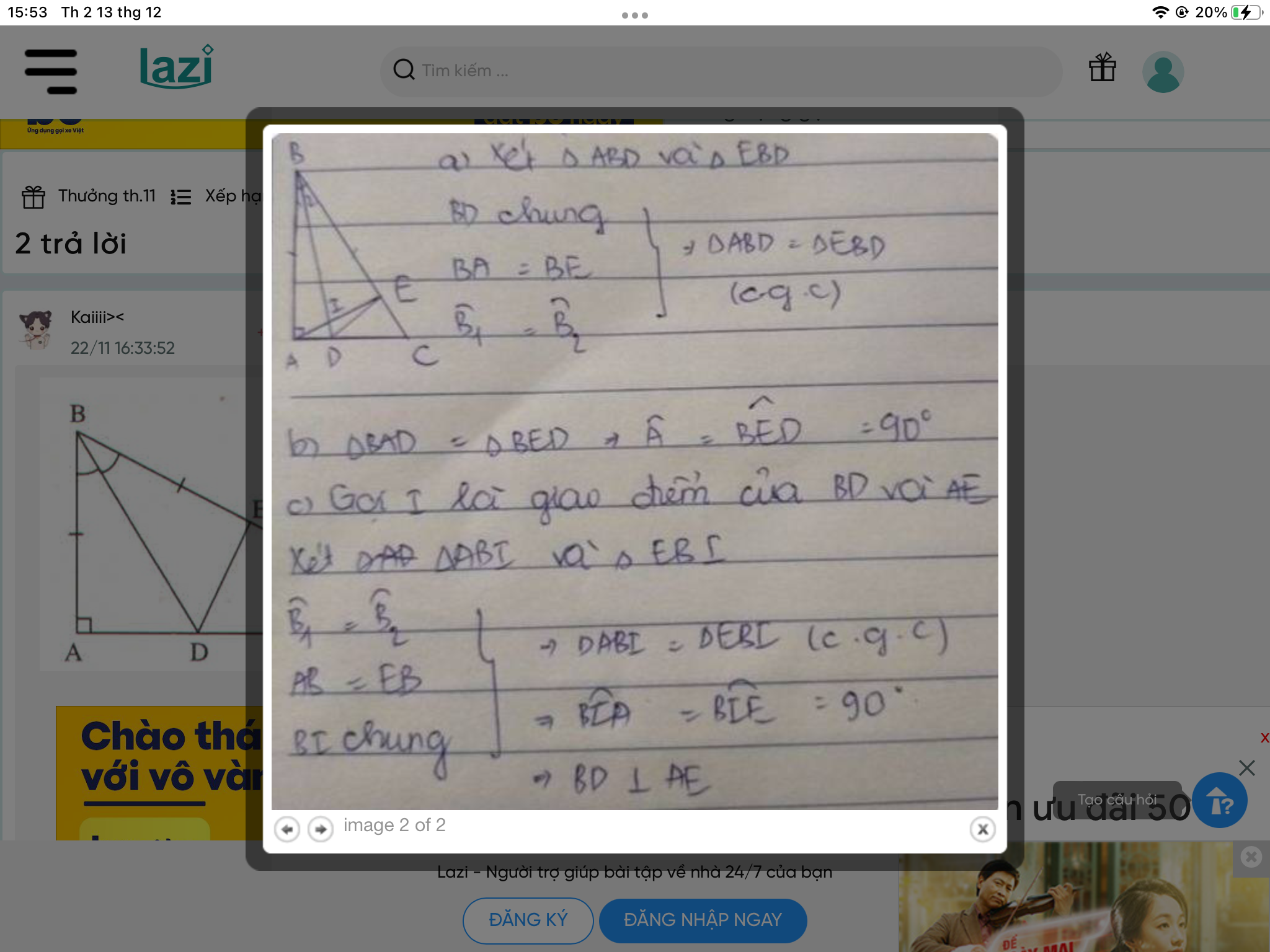
Cho tam giác ABC vuông tại A(AB<AC). Tia phân giác góc B cắt cạnh AC tại D, trên cạnh BC lấy điểm E sao cho AB=BE
a/ CMR;tam giác ABD= tam giác EBD, Tính số đo góc BED
b/Gọi I là giao điểm của đường thẳng ED và đường thẳng AB . Chứng minh AI=EC
c/ Vẽ AH vuông góc với BC . Chứng minh AE là tia phân giác của góc HAD