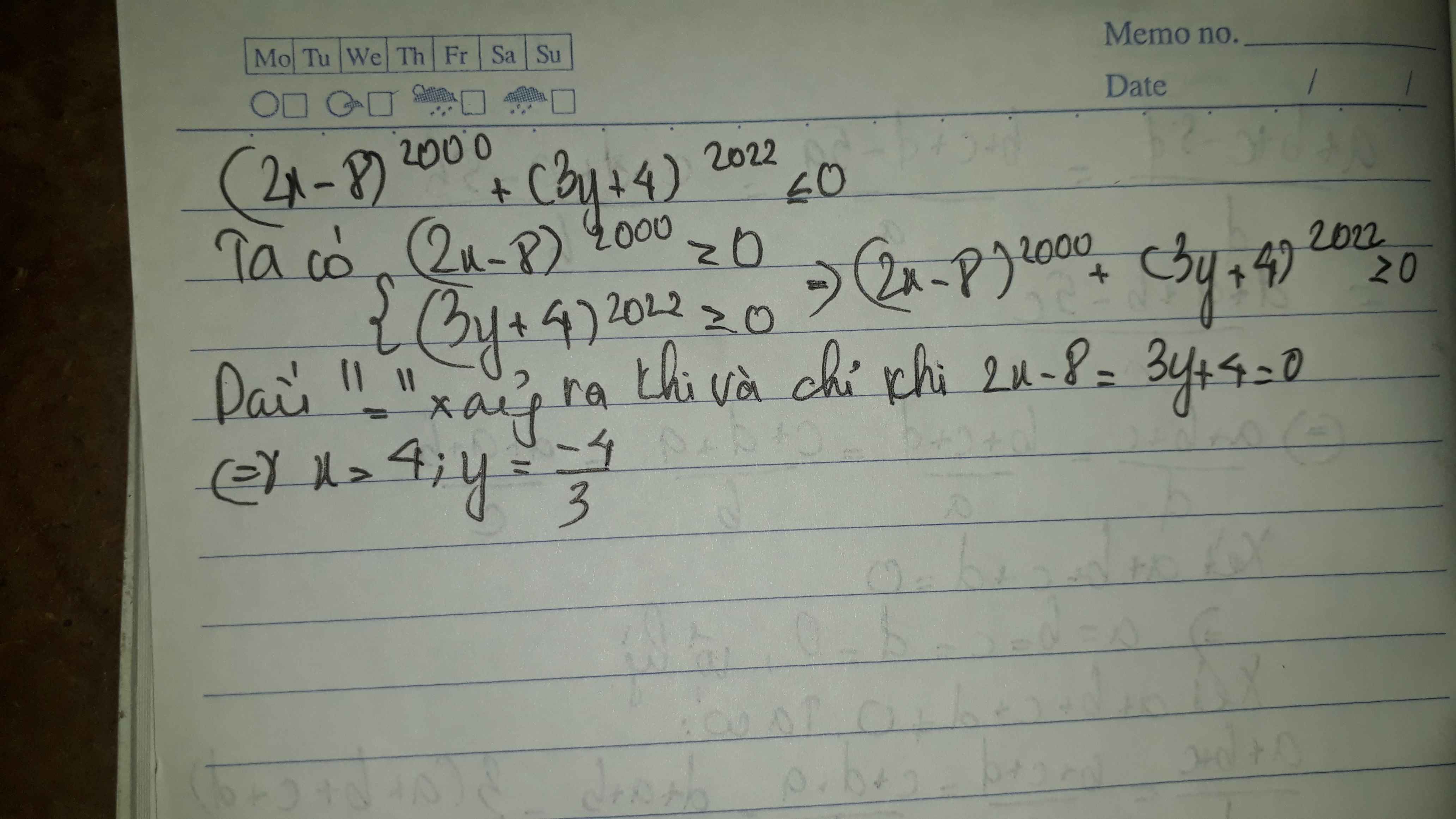(2x-5)2000+(3y + 4)2002 nhỏ hơn hoặc bằng 0

Những câu hỏi liên quan
Tìm x,y biết:(2x-5)^2000+(3y+4)^2002 nhỏ hơn hoặc bằng 0
Tìm x,y biết:
(2x-5)^2000+(3y+4)^2002 bé hơn hoặc bằng 0
(2x - 5)2000 + (3y + 4)2002
ta có: (2x - 5)2000 \(\ge\) 0 ; (3y + 4)2002 \(\ge\) 0
=> (2x - 5)2000 + (3y + 4)2002 \(\ge\) 0
Dấu "=" xảy ra khi 2x - 5 = 0 và 3y + 4 = 0
=> 2x = 5 và 3y = -4
=> x = 2,5 và y = \(\frac{-4}{3}\)
Đúng 0
Bình luận (0)
bé hơn mà có phải lớn hơn 0 đâu ?
Do(2x-5)^2020 lớn hơn hoặc =0
(3y+4)^2002 lớn hơn hoặc =0
suy ra (2x-5)^2020+(3y+4)^2002 lớn hơn hoặc =0
dấu ''='' xảy ra khi
2x-5=0 2x=5 x=5/2
3y+4=0 3y=-4 y=-4/3
Đúng 0
Bình luận (0)
Tìm x,y biết: (2x-5)^2000+(3y+4)^2002 nhỏ hơn bằng 0
\(\left(2x-5\right)^{2000}\ge0\forall x;\left(3y+4\right)^{2002}\ge0\forall y\Rightarrow\left(2x-5\right)^{2000}+\left(3y+4\right)^{2000}\ge0\forall x,y\)
Kết hợp giả thiết ta có:\(2x-5=0;3y+4=0\Rightarrow x=\frac{5}{2};y=-\frac{4}{3}\)
(2x - 5)2000 + (3y + 4)2002 Bé hơn hoặc bằng 0
Có :
\(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\ge0\)
Mà theo đề bài : \(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\le0\)
\(\Rightarrow\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}=0\)
\(\Leftrightarrow\hept{\begin{cases}2x-5=0\\3y+4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=-\frac{4}{3}\end{cases}}\)
Đúng 0
Bình luận (0)
A) Tìm x, y biết (2x-5)2000+(3y+4)2002 bé hơn hoặc bằng 0. B) Tìm các số nguyên dương m, n sao cho 2m-2n=256
Các bạn trả lời cho mình đi mình sẽ k cho bạn
Đúng 0
Bình luận (0)
\(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\le0\) (1)
có : \(\left(2x-5\right)^{2000}\ge0\forall x\)
\(\left(3y+4\right)^{2002}\ge0\forall x\)
\(\Rightarrow\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\ge0\) (2)
\(\left(1\right)\left(2\right)\Rightarrow\left(2x-5\right)^{2000}+\left(3y-4\right)^{2002}=0\)
\(\Rightarrow\hept{\begin{cases}\left(2x-5\right)^{2000}=0\\\left(3y+4\right)^{2002}=0\end{cases}\Rightarrow\hept{\begin{cases}2x-5=0\\3y+4=0\end{cases}\Rightarrow}\hept{\begin{cases}x=\frac{5}{2}\\y=-\frac{4}{3}\end{cases}}}\)
Đúng 0
Bình luận (0)
Tìm x;y biết: (2x-5)2000 + (3y+4)2002 < hoặc = 0
Do (2x-5)2000>0
(3y+4)2002>0
Mà (2x-5)2000+(3y+4)2002<0
=>(2x-5)2000=0 (3y+4)2002=0
<=>x=2,5 y=4/3
Đúng 0
Bình luận (0)
1)Tìm n thuộc Z biết:3^-2*3^4*3^n=3^7
2)Tìm x thuộc Q biết:(7x+2)^-1=3^-2
3)Tìm x,y thuộc Z biết:(2x-5)^2000+(3y+4)^2002 bé hơn hoặc bằng 0.
\(\)\(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}< 0\)
x và y nhỏ hơn hoặc bằng 0 nha mn
ai nhanh mk tick và kết bạn nha
Ta có :\(\left(2x-5\right)^{2000}\) \(\geq\) \(0\) \(;\) \(\left(3y+4\right)^{2002}\) \(\geq\) \(0\)
\(\implies\) \(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\) \(\geq\) \(0\) (1)
Mà theo đầu bài ra ta có: \(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\) <\(0\) (2)
Từ (1);(2) \(\implies\) Không có số nguyên x;y nào nhỏ hơn hoặc bằng 0 thỏa mãn ycbt
tìm x,y biết ( 2x - 8 ) mũ 2000 + ( 3y + 4 ) mũ 2022 bé hơn hoặc bằng 0
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)