Cho góc nhìn xOy , kể thêm tia phân giác Oz. Trên tia Ox lấy A, Oy lấy B sao cho OA=OB. Trên Oz lấy điểm I bất kì. Chứng minh OI là đường trung trực của AB

Những câu hỏi liên quan
4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a. Δ AOI = Δ BOI.
b. AB ⊥ OI.
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
Đúng 1
Bình luận (0)
Cho góc xOy, gọi Oz là tia phân giác góc xOy. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA=OB. Lấy điểm I trên Oz sao cho OI > OA
a) So sánh IA và IB
b) Chứng minh Oz là trung trực của AB
Giúp mình bài này với ạ
a: Xét ΔAOI và ΔBOI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔAOI=ΔBOI
Suy ra: IA=IB
Đúng 1
Bình luận (0)
cho góc nhọn xOy và tia phân giác Oz của góc đó .Trên tia Ox lấy điểm a ,trên tia Oy lấy điểm b sao cho oa=ob . trên tia Oz lấy điểm I bất kì chứng minh a) tam giác AOI = tam giác BOI
B) AB VUÔNG GÓC OI
Ta có hình vẽ:
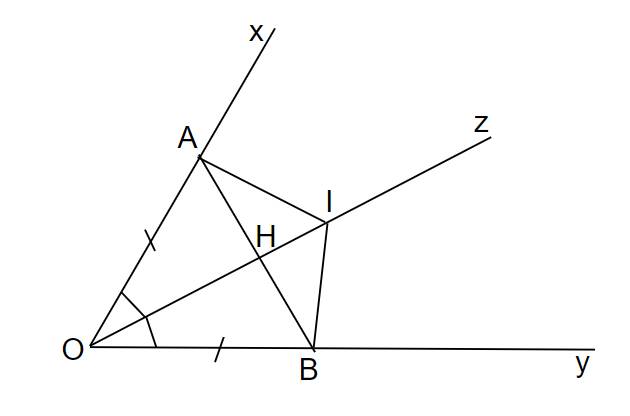
a) Vì Oz là phân giác của xOy nên
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=>
Đúng 0
Bình luận (0)
Vẽ xOy ,Vẽ tia phân giác Oz của xOy .lấy điểm A trên tia Ox ,điểm B trên tia Oy sao cho OA = OB .Lấy điểm C trên tia Oz sao cho OC < OA
a) Chứng minh: CA = CB
b) AB cắt Oz Tại I .Chứng minh: Tam giác OAI = tam giác OBI ; OI là đường trung trực của đoạn thẳng AB
cho góc xoy và tia phân giác oz của góc đó. Trên ox, lấy điểm A, trên oy lấy điểm B sao cho OA=OB . trên tia oz lấy điểm I bất kì. chúng minh:
a, tam giác AOI= tam giác BOI
b, AB vuông góc OI
Cho góc nhọn xoy và tia phân giác Oz của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB, trên tia Oz lấy điểm I bất kỳ. Chứng minh rằng:
a)Tam giác AOI = Tam giác BOI
b) AB vuông góc với OI
cho góc xoy. gọi Oz là tia phân giác của nó . Trên tia Ox lấy điểm A, Trên Oy lấy điểm B sao cho OA=OB. M là 1 điểm bất kỳ trên Oz(M khác O)
chứng minh tia OM là phân giác của AMB và đường thẳng Om là trung trực của đoạn AB
cho góc xoy. gọi Oz là tia phân giác của nó . Trên tia Ox lấy điểm A, Trên Oy lấy điểm B sao cho OA=OB. M là 1 điểm bất kỳ trên Oz(M khác O)
chứng minh tia OM là phân giác của AMB và đường thẳng Om là trung trực của đoạn AB
Xét \(\Delta\)AOM và \(\Delta\)BOM có:
OA=OB (gt)
góc AOM=góc BOM (do Oz là phân giác góc xOy)
OM chung
=> \(\Delta\)AOM = \(\Delta\)BOM (c.g.c) (1)
(1) => góc AMO=góc BMO (2 góc tương ứng)
=> MO là phân giác góc AMB (dpcm)
(1) => AM=BM (2 góc tương ứng)
=> \(\Delta\)ABM cân tại M (dhnb)
Xét \(\Delta\)ABM cân tại M có tia phân giác MO đồng thời là đường trung trực của cạnh AB (t/c các đường đặc biệt trong \(\Delta\)cân) (dpcm)
Đúng 0
Bình luận (0)
cho góc xooy nhọn oz là tia phan giác của góc xoy trên tia ox lấy điểm a trên tia oy lấy điểm B sao cho OA bằng OB . GỌI M là giao điểm của AB và tia OZ . hỏi chứng minh OZ là đường trung trực củA đoạn thẳng AB; trên tia Oz lấy điểm y sao cho M là trung điểm của Oy , chứng minh AI song song OB













