x0. x2. x4. x6… x98. x100 = 22510 : 23. 243 ( x khác 0 )

Những câu hỏi liên quan
Cho các số tự nhiên x1,x2,..,x101x1,x2,..,x101 thỏa mãn x1+x2+x3+x4+...+x99+x100+x101=0x1+x2+x3+x4+...+x99+x100+x101=0 và x1+x2=x3+x4=...=x97+x98=x99+x100=x100+x101=1.x1+x2=x3+x4=...=x97+x98=x99+x100=x100+x101=1. Số nguyên x100x100 bằng bao nhiêu ?
Tính nhanh
\(\frac{1}{2}x4+\frac{1}{4}x6+\frac{1}{6}x8+...............+\frac{1}{96}x98+\frac{1}{98}x100\)
Tính giá trị của các đa thức sau: x2 + x4 + x6 + x8 + … + x100 tại x = -1
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 = 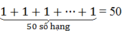
Vậy giá trị đa thức bằng 50 tại x = -1.
Đúng 0
Bình luận (0)
Cho các đa thức: f(x) = 1 + x + x2 +...+ x100; g(x) = x2 + x4 + x6 +...+ x100
Tính giá trị của f(x) – g(x) tại x = –1
f(-1)= 1+(-1)+(-1)2+...+(-1)100
=1+(-1)+1+...+1
=1+0
=1
Đúng 0
Bình luận (0)
Cho các đa thức: f(x) = 1 + x + x2 +...+ x100; g(x) = x2 + x4 + x6 +...+ x100
Tính giá trị của f(x) – g(x) tại x = –1
A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49
Đúng 0
Bình luận (0)
2 x 3 x4 x5 x6 x ...x100 x(x - 2)=0
\(2\times3\times4\times5\times6\times...\times100\times\left(x-2\right)=0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=0+2\)
\(\Rightarrow x=2\)
Vậy x = 2
_Chúc bạn học tốt_
Đúng 0
Bình luận (0)
2 x 3 x4 x5 x6 x ...x100 x(x - 2)=0
Đặt 2x3x4x5x...x100 là A, ta có :
A x ( x - 2 ) = 0
=> x - 2 = 0
x = 0 + 2
x = 2
Đúng 0
Bình luận (0)
=> X-2=0( vì 2×3...×100 >0)
=> X=0+2
=> X=2
Vậy X=2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. cho 6 số khác 0 x1,x2,x3,x4,x5,x6 thỏa mãn điều kiện
x2 mũ 3 = x1.x3, x3 mũ 2 =x2.x4
x4 mũ 2 = x3.x5 , x5 mũ 2 = x4.x6
Cho sáu số khác 0:x1;x2;x3;x4;x5;x6 thoả mãn các điều kiện: x22=x1x3 x32=x2x1 x42=x3x5 x52=x4x6 CMR:
x1/x6=[x1+...+x/x2+....+x6]^5
Bài 1 : Cho a,b,c là các số hữu tỉ khác 0 sao cho a+b-c/c=a-b+c/b=(-a)+b+c/a
Tính giá trị của biểu thức A=(a+b).(b+c).(c+a)/abc
(LƯU Ý : DẤU / LÀ ...TRÊN.....)
Bài 2 : Cho x,x2,x3,x4,x5,x6 thỏa mãn :
(x2)^2=x1.x3
(x3)^2=x2.x4
(x4)^2=x3.x5
(x5)^2=x4.x6
Chứng minh rằng : x1/x6=(x1+x2+x3+x4+x5/x2+x3+x4+x5+x6)^5
Giusp mk vs nhé các bn !!!
Cho x1, x2, x3, x4, x5, x6 là các số đôi một khác nhau thuộc tập {1, 2, 3, 4, 5, 6} và thỏa mãn x1-5x2+10x3-10x4+5x5-x6=0. Hỏi có bao nhiêu cách chọn bộ (x1, x2, x3, x4, x5, x6)?

















