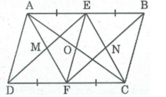
+) Ta có:

AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).

Và AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF

Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành

⇒ AF //CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE = 1/2 AB (gt)

DF = 1/2 CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)

SBT.

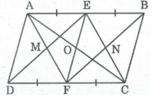
Gọi O là giao điểm của AC và EF

Tứ giác AECF là hình bình hành ⇒ OE = OF

Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Suy ra: MN đi qua trung điểm O của EF.

Vậy AC, EF, MN đồng quy tại O.

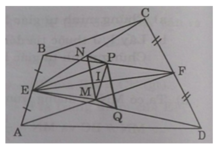
a) Xét tam giác ABF có:

E là trung điểm của AB

P là trung điểm của BF

⇒ EP là đường trung bình của ΔABF

⇒ EP // AF và EP = AF/2

M là trung điểm AF (gt)

⇒ MF = AF/2

Do đó EP // MF và EP = MF. Vậy EPFM là hình bình hành

I là giao điểm của hai đường chéo MP và EF nên I là trung điểm của MP.

b) Do tứ giác EPFM là hình bình hành nên I là trung điểm của EF.

Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm của EF ⇒ I là trung điểm của NQ (2)

Từ (1) và (2) ⇒ MNPQ là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).

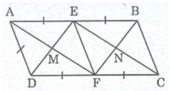
Tứ giác AEFD là hình thoi

⇒ AF ⊥ ED ⇒  ∠ (EMF) = 90 0

AF // CE (vì tứ giác AECF là hình bình hành)

Suy ra: CE ⊥ ED ⇒  ∠ (MEN) =  90 0

Xét tứ giác EBFD, ta có: EB = FD (vì cùng bằng AE)

EB // FD (vì AB // CD)

Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF

Suy ra: BF ⊥ AF ⇒ ∠ (MFN) = 90 0

Vậy tứ giác EMFN là hình chữ nhật.

làm đc mỗi câu b :))

AEFC là hình bình hành ( tự cm nhá :) )

=> đường chéo AC giao đường chéo EF tại trung điểm của EF

câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF

=> ĐPCM

câu b thui, câu a lằng nhằng quá lười nghĩ thông cảm nhé