Cho hình bình hành ABCD có A(-1;3) , B(2;4) , C(0;1). Tìm tọa độ đỉnh D và tọa độ tâm I của hình bình hành

Những câu hỏi liên quan
Cho hình bình hành ABCD có cạnh AB=15,1 cm AB=AD và A=60 độ . Tính S phần không chung nhau giữa hình bình hành ABCD và hình tròn nội tiếp hình bình hành ABCD
bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có A =90, biết AB=3cm, AC=5cm.Khi đó diện tích hình bình hành ABCD là ?
hình bình hành ABCD là hình chữ nhật( vì có 1 góc vuông)
Diện tích hình chữ nhật ABCD là
S= AB *AC= 3*5= 15 cm vuông
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho hình bình hành ABCD có
A
^
120
0
, các góc còn lại của hình bình hành là? A.
B
^
60
0
,
C
^
120
0
,
D
^
60
0
B.
B
^...
Đọc tiếp
Cho hình bình hành ABCD có A ^ = 120 0 , các góc còn lại của hình bình hành là?
A. B ^ = 60 0 , C ^ = 120 0 , D ^ = 60 0
B. B ^ = 90 0 , C ^ = 120 0 , D ^ = 60 0
C. B ^ = 60 0 , C ^ = 120 0 , D ^ = 75 0
D. B ^ = 60 0 , C ^ = 45 0 , D ^ = 60 0

Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
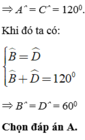
Đúng 0
Bình luận (0)
Cho HÌnh bình hành ABCD , góc ADC=1/2 góc D. Gọi M là trung điểm của AB. 2 tia DA và CM cắt nhau tại E
a) Chứng Minh: tứ giác AEBC là hình bình hành
b) Hình bình hành ABCD phải có thêm điều kiện gì để hình bình hành AEBC là hình chữ nhật
Cho hình bình hành ABCD có độ dài cạnh AB là a,cạnh BC là b,Cạnh a=8cm,Cạnh b=3cm.Tính Chu vi và diện tích hình bình hành ABCD?
Cho hình bình hành ABCD có chiều cao AH = 9 cm cạnh đáy AB gấp đôi chiều cao AH cạnh bên BC kém cạnh đáy AB là 3 cm a Tính diện tích hình bình hành ABCD B tính chu vi hình bình hành abcd
a) Cạnh đáy AB là: 9 x 2 =18(cm)
Cạnh bên BC là: 18 - 3 = 15(cm)
Diện tích hình bình hành ABCD là: 18 x 9 = 162(cm2)
b) Chu vi hình bình hành ABCD là: (18 + 15) x 2 = 66(cm)
Đ/S: a) 162 cm2
b) 66 cm
Bài 1: Cho hình bình hành ABCD , đường chéo BD . Kẻ AH và CK vuông góc với BD tại H và K . Chứng minh tứ giác AHCK là hình bình hành. Bài 2: Cho hình bình hành ABCD có M N, lần lượt là trung điểm của AB CD , . AN và CM cắt BD lần lượt tại E và F . a) Chứng minh AMCN là hình bình hành. ( Hình 6) b) Từ F kẻ đường thẳng song song với AB cắt AN tại G. Chứng minh BF FE ED . Bài 3: Cho tam giác ABC cân tại A , lấy điểm D trên cạnh AB , điểm E trên cạnh AC sao cho BD CE . a) Tứ giác BDEC là hì gì...
Đọc tiếp
Bài 1: Cho hình bình hành ABCD , đường chéo BD . Kẻ AH và CK vuông góc với BD tại H và K . Chứng minh tứ giác AHCK là hình bình hành. Bài 2: Cho hình bình hành ABCD có M N, lần lượt là trung điểm của AB CD , . AN và CM cắt BD lần lượt tại E và F . a) Chứng minh AMCN là hình bình hành. ( Hình 6) b) Từ F kẻ đường thẳng song song với AB cắt AN tại G. Chứng minh BF FE ED . Bài 3: Cho tam giác ABC cân tại A , lấy điểm D trên cạnh AB , điểm E trên cạnh AC sao cho BD CE . a) Tứ giác BDEC là hì gì? Vì sao? b) Các điểm D E, ở vị trí nào thì BD DE EC
Bài 3:
a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Hình thang BDEC có \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Để BD=DE=EC thì BD=DE và DE=EC
BD=DE thì ΔDBE cân tại D
=>\(\widehat{DBE}=\widehat{DEB}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(hai góc so le trong, DE//BC)
nên \(\widehat{DBE}=\widehat{EBC}\)
=>\(\widehat{ABE}=\widehat{EBC}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Xét ΔEDC có ED=EC
nên ΔEDC cân tại E
=>\(\widehat{EDC}=\widehat{ECD}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ECD}=\widehat{DCB}\)
=>\(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác từ C kẻ xuống AB
Bài 2:
a: Ta có: ABCD là hình bình hành
=>AB//CD và AB=CD(1)
Ta có: M là trung điểm của AB
=>\(AM=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của CD
=>\(NC=ND=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AM=MB=NC=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có AMCN là hình bình hành
=>AN//CM
Xét ΔDFC có
N là trung điểm của DC
NE//FC
Do đó: E là trung điểm của DF
=>DE=EF(4)
Xét ΔABE có
M là trung điểm của BA
MF//AE
Do đó: F là trung điểm của BE
=>BF=FE(5)
Từ (4) và (5) suy ra BF=FE=ED
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có cạnh AB = 10 3 c m , AD = 8cm, A ^ = 60°. Tính diện tích của hình bình hành
Kẻ DH ^ AB tại H
⇒ A H = A D 2 = 4 c m
Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.
ÞSABCD = DH.AB = 120cm2
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc a = 3 góc B . Tính số đo các góc của hình bình hành
\(\widehat{A}=\widehat{C}=135^0\)
\(\widehat{B}=\widehat{D}=45^0\)
Đúng 0
Bình luận (0)




















