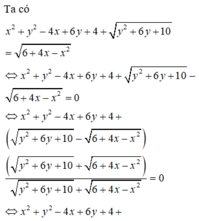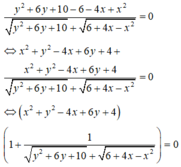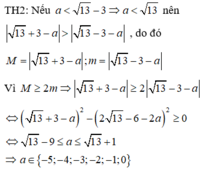Cho phương trình (x2 -3x+m) +x2 -8x+2m. Có bao nhiêu giá trị nguyên của thẩm số m thuộc đoạn [-20;20] để hàm số có 4 nghiệm
Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình
log
2
(
x
2
-
3
x
+
2
m
)
log
2
(
x
+
m
)
có nghiệm thực A. Mười. B. Chín. C. Vô số. D. Tám
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình log 2 ( x 2 - 3 x + 2 m ) = log 2 ( x + m ) có nghiệm thực
A. Mười.
B. Chín.
C. Vô số.
D. Tám
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình
x
+
2
-
x
2
+
1
2
+
18
(
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình
x + 2 - x 2 + 1 2 + 18 ( x 2 + 1 ) x 2 + 1 x + 2 + x 2 + 1 = m ( x 2 + 1 ) có nghiệm thực?
A. 25
B. 2019
C. 2018
D. 2012
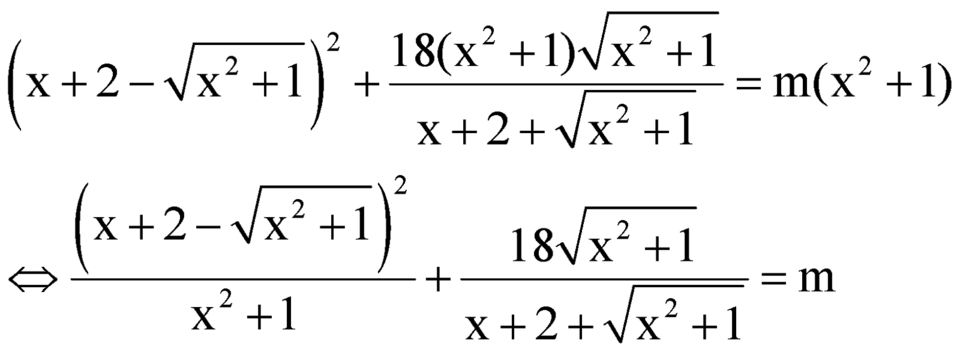
Đặt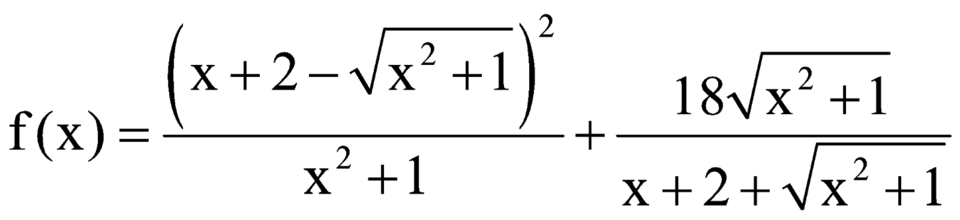 
.
Sử dụng chức năng MODE 7,
ta tìm 
Để phương trình 
có nghiệm
.
Kết hợp điều kiện ta có 
.
Vậy có 
giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn D
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình
(
x
+
2
-
x
2
+
1
)
2
+
18
(
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình ( x + 2 - x 2 + 1 ) 2 + 18 ( x 2 + 1 ) x 2 + 1 x + 2 + x 2 + 1 = m ( x 2 + 1 ) có nghiệm thực?
A. 25
B. 2019
C. 2018
D. 2012
Có bao nhiêu giá trị nguyên của tham số m để phương trình
9
1
+
1
-
x
2
-
m
+
3
.
3
1
+
1
-...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 9 1 + 1 - x 2 - m + 3 . 3 1 + 1 - x 2 + 2 m + 1 = 0 có nghiệm thực?
A. 5
B. 7
C. Vô số
D. 3
Có bao nhiêu giá trị nguyên của tham số m để phương trình
9
1
+
1
-
x
2
-
m
+
3
3
1
+
1
-
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 9 1 + 1 - x 2 - m + 3 3 1 + 1 - x 2 + 2 m + 1 = 0 có nghiệm thực?
A. 5
B. 7
C. Vô số
D. 3
Cho bất phương trình
3
+
x
+
6
-
x
-
18
+
3
x
-
x
2
≤
m
2
-
m
+
1
(m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi...
Đọc tiếp
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt 
Suy ra 
Ta có 
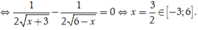
Ta có bảng biến thiên
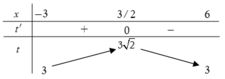
Từ bảng biến thiên ta suy ra 
Khi đó bất phương trình trở thành: 
Xét hàm số 
với 
Ta có 
Suy ra hàm số f(t) nghịch biến trên 
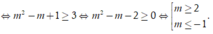
Chọn C.
Đúng 0
Bình luận (0)
Cho phương trình
x
3
-
3
x
2
+
m
x
-
2
m
+
2
0
(m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 t...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 + m x - 2 m + 2 = 0 (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x1<1<x2<x3?
A.0
B.3
C.5
D.Vô số
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.
Đúng 0
Bình luận (0)
Tập nghiệm của pt: x4-8x ²-90Hệ pt: x2+y2+xy7 x2+y2-xy3có nghiệm là.Cho phương trình(x2-3x+3)2-2x2+6x-50 Nếu đặt tx2-3x+3thì phương trình đã cho trở thành phương trình nào Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằngA. -3.B. 2.C. 18.D. 21.
Đọc tiếp
Tập nghiệm của pt: x4-8x ²-9=0
Hệ pt: x2+y2+xy=7
x2+y2-xy=3
có nghiệm là.
Cho phương trình(x2-3x+3)2-2x2+6x-5=0 Nếu đặt t=x2-3x+3
thì phương trình đã cho trở thành phương trình nào
Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2
có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằng
A. -3.
B. 2.
C. 18.
D. 21.
Cho hai số thực x, y thỏa mãn
x
2
+
y
2
-
4
x
+
6
y
+
4
+
y
2
+
6
y
+
10
6
+
4
x
-
x
2...
Đọc tiếp
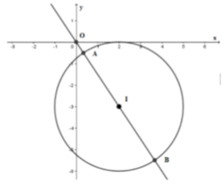
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
Đúng 0
Bình luận (0)