Tính chu vi hình tứ giác ABCD là:14,27,38,50,65,96

Những câu hỏi liên quan
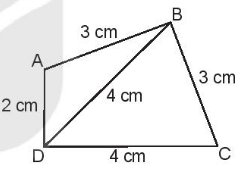
a) Tính chu vi hình tam giác ABD và chu vi hình tam giác BCD.
b) Tính chu vi hình tứ giác ABCD.
c) Số?
Tổng chu vi của các hình tam giác ABD và BCD hơn chu vi hình tứ giác ABCD là (?) cm
a)
Chu vi hình tam giác ABD là:
3 + 4 + 2 = 9 (cm)
Chu vi hình tam giác BCD là:
4 + 3 + 4 = 11 (cm)
b)
Chu vi hình tứ giác ABCD là:
3 + 3 + 4 + 2 = 12 (cm)
c)
Tổng chu vi của tam giác ABD và BCD là:
9 + 11 = 20 (cm)
Tổng chu vi của tam giác ABD và BCD hơn chu vi hình tứ giác ABCD là:
20 – 12 = 8 (cm)
Đúng 0
Bình luận (0)
1.Cho tam giác ABCD biết cạnh AB 15dm; BC 235cm; CD 2m, AD 321cm. Tính chu vi hình tam giác2.Một hình tứ giác có 4 cạnh bằng nhau và bằng 181cm. Tính chu vi hình tứ giác đó.3. Hình tứ giác nếu giảm cạnh thứ nhất đi 54cm, giảm cạnh thứ hai đi 24cm, tăng cạnh thứ ba và cạnh thứ tư mỗi cạnh thêm 9dm thì chu vi hình tứ giác là 589cm. Hỏi nếu tăng mỗi cạnh của hình tứ giác lên 67cm thì chu vi hình tứ giác đó bằng bao nhiêu.4.Một hình tứ giác nếu giảm cạnh thứ nhất đi 12dm, tăng cạnh thứ hai thêm...
Đọc tiếp
1.Cho tam giác ABCD biết cạnh AB = 15dm; BC= 235cm; CD = 2m, AD = 321cm. Tính chu vi hình tam giác
2.Một hình tứ giác có 4 cạnh bằng nhau và bằng 181cm. Tính chu vi hình tứ giác đó.
3. Hình tứ giác nếu giảm cạnh thứ nhất đi 54cm, giảm cạnh thứ hai đi 24cm, tăng cạnh thứ ba và cạnh thứ tư mỗi cạnh thêm 9dm thì chu vi hình tứ giác là 589cm. Hỏi nếu tăng mỗi cạnh của hình tứ giác lên 67cm thì chu vi hình tứ giác đó bằng bao nhiêu.
4.Một hình tứ giác nếu giảm cạnh thứ nhất đi 12dm, tăng cạnh thứ hai thêm 47cm, giảm cạnh thứ ba đi 1m thì chu vi hình tứ giác là 342cm. Hỏi nếu tăng mỗi cạnh lên 5dm thì chu vi hình tứ giác bằng bao nhiêu?
5.Cho hình tứ giác ABCD có cạnh AB = 35dm. Biết cạnh BC dài hơn cạnh AB là 56cm nhưng bằng nửa CD. Cạnh AD ngắn hơn cạnh CD là 4m. Tính chu vi hình tứ giác ABCD đó.
6.Tính chu vi hình tứ giác có 4 cạnh bằng nhau và bằng 348cm.
tứ giác ABCD có tọa độ các đỉnh A(0,-4),B(3,0),C(0,4),D(-3,0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó
Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:
AB2=OA2+OB2
AB2=42+32 = 16 + 9 = 25
AB = √25
Vậy chu vi của hình thoi bằng 4√25
Tứ giác ABCD có tọa độ các đỉnh như sau A(0;2); B(3; 0); C(0;-2) ; D(-3;0).Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.
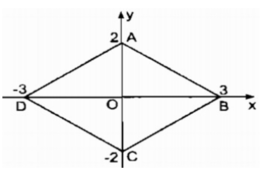
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13
Đúng 0
Bình luận (0)
tứ giác ABCD có tọa độ các đỉnh như sau A(0:2) , B(3:0) , C(0:-2) , D(-3:0) . tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.
Cho hình vẽ:
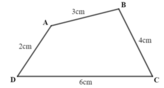
Tính chu vi của hình tứ giác ABCD
Chu vi tứ giác ABCD là:
2 + 3 + 4 + 6 = 15 (cm)
Đáp số: 15cm
Đúng 0
Bình luận (0)
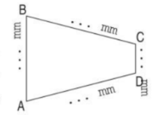
a) Đo độ dài các cạnh của hình tứ giác ABCD rồi viết số thích hợp vào chỗ chấm.
b) Tính chu vi hình tứ giác ABCD.
Phương pháp giải:
- Dùng thước kẻ đo chiều dài của mỗi cạnh rồi điền vào chỗ trống.
- Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Lời giải chi tiết:
a) Độ dài các cạnh của hình tứ giác đo được là:
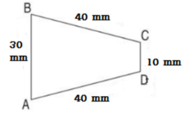
b) Chu vi hình tứ giác ABCD là :
40 + 10 + 40 + 30 = 120 (mm)
Đáp số: 120mm.
Đúng 0
Bình luận (0)
a) Đo độ dài các cạnh của hình tứ giác ABCD rồi viết số thích hợp vào chỗ chấm.
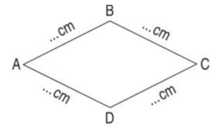
b) Tính chu vi hình tứ giác ABCD.
Phương pháp giải:
- Dùng thước kẻ đo độ dài các cạnh của hình tứ giác rồi điền vào chỗ trống.
- Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Lời giải chi tiết:
a)
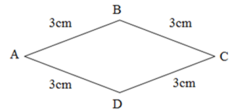
b)
Chu vi hình tứ giác ABCD là :
3 + 3 + 3 + 3 = 12 (cm)
Đáp số: 12 cm.
Đúng 0
Bình luận (0)
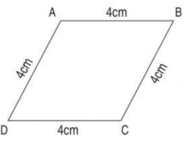
a) Tính độ dài đường gấp khúc ABCD.
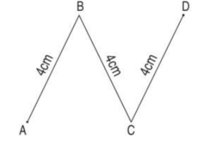
b)Tính chu vi hình tứ giác ABCD.
Phương pháp giải:
Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó (cùng đơn vị đo).
Lời giải chi tiết:
a) Độ dài đường gấp khúc ABCD là:
4 + 4 + 4 + 4 = 16 (cm)
Đáp số: 16 cm.
Cách khác:
Độ dài đường gấp khúc ABCD là:
4 x 4 = 16 (cm)
Đáp số: 16cm.
b)
Chu vi tứ giác ABCD là:
4 + 4 + 4 + 4 = 16 (cm)
Đáp số: 16cm.
Cách khác:
Chu vi tứ giác ABCD là:
4 x 4 = 16 (cm)
Đáp số: 16cm.
Đúng 0
Bình luận (0)











