pH của CH3COOH 0.01M là bnhju và cách tính
E được chỉ là pH>2-> Nồng độ H+ <0,01 mà k hiểu ai giải và giải thích dùm e với ạ 😭😭😭
Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
a) Ta có:\(-\log\left[H^+\right]=6.1\Leftrightarrow-\log x=6,1\)
b) Phương trình vừa tìm được có ẩn là x và nằm ở vị trí hệ số của logarit
Có 5 dung dịch NH3, HCl, NH4Cl, Na2CO3, CH3COOH cùng nồng độ được đánh ngẫu nhiên là A, B, C, D, E. Giá trị pH và khả năng dẫn điện của dung dịch theo bảng sau:
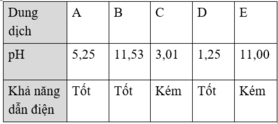
Các dung dịch A, B, C, D, E lần lượt là
A. NH4Cl, NH3, CH3COOH, HCl, Na2CO3
B. CH3COOH, NH3, NH4Cl, HCl, Na2CO3
C. NH4Cl, Na2CO3, CH3COOH, HCl, NH3
D. Na2CO3, HCl, NH3, NH4Cl, CH3COOH
Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức \(pH = - \log x\), trong đó \(x\) là nồng độ ion H+ tính bằng mol/L.
Biết sữa có độ pH là 6,5. Nồng độ H+ của sữa bằng bao nhiêu?
tham khảo
Ta có:
\(pH=-logx\Leftrightarrow6,5=-logx\Leftrightarrow logx=-6,5\Leftrightarrow x=10^{-6,5}\approx3,16.10^{-77}\)
Vậy nồng độ \(H^+\) của sữa bằng \(3,16.10^{-7}\) mol/L.
Trong một dung dịch CH3COOH người ta xác định được nồng độ H+ bằng 3,0.10-3M và nồng độ CH3COOH bằng 3,93.10-1M. Nồng độ mol ban đầu của CH3COOH là:
A. 0,390M
B. 0,393M
C. 0,396M
D. 0,399M
Có 5 dung dịch NH3, HCl, NH4Cl, Na2CO3, CH3COOH cùng nồng độ được đánh ngẫu nhiên là A, B, C, D, E. Giá trị pH và khả năng dẫn điện của dung dịch theo bảng sau:
| Dung dịch |
A |
B |
C |
D |
E |
| pH |
5,25 |
11,53 |
3,01 |
1,25 |
11,00 |
| Khả năng dẫn điện |
Tốt |
Tốt |
Kém |
Tốt |
Kém |
Các dung dịch A, B, C, D, E lần lượt là
A. NH4Cl, NH3, CH3COOH, HCl, Na2CO3
B. NH4Cl, Na2CO3, CH3COOH, HCl, NH3
C. CH3COOH, NH3, NH4Cl, HCl, Na2CO3
D. Na2CO3, HCl, NH3, NH4Cl, CH3COOH
Cho 2 dung dịch HCl và CH3COOH có cùng nồng độ. Dung dịch HCl có pH = x, dung dịch CH3COOH có pH = y. Bỏ qua sự điện li của nước, các dung dịch ở cùng nhiệt độ phòng. Biết ở nhiệt độ phòng, cứ 100 phân tử CH3COOH thì có 1 phân tử phân li ra ion. Mối liên hệ của x và y là:
A. x = y - 2
B. y = x – 2
C. x = 2y
D. y = 2x
Không mất tính tổng quát, ta đặt:
![]()
Vì HCl là chất điện li mạnh nên ta có phương trình điện li như sau:
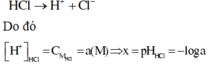
Vì CH3COOH là chất điện li yếu nên ta có phương trình điện li như sau
Xét cân bằng điện li: CH3COOH ⇌ CH3COO- + H+
Nồng độ ban đầu: aM 0
Nồng độ phân li: 0,01a M → 0,01a M
Nồng độ cân bằng: 0,99a M 0,01a M
Ta có
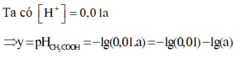
![]()
Đáp án A.
Độ pH của một chất được xác định bởi công thức pH = -log[H+] trong đó H+ là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H+ của một chất biết rằng độ pH của nó là 8,06
A. 8 , 7 . 10 - 9 mol/L
B. 2 , 44 . 10 - 7 mol/L
C. 2,74,4 mol/L
D. 3 , 6 . 10 - 7 mol/L
Độ pH của một chất được xác định bởi công thức pH = -log[H+] trong đó [H+] là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H+ của một chất biết rằng độ pH của nó là 2,44
A. 1,1.108 mol/L
B. 3,2.10-4 mol/L
C. 3,6.10-3 mol/L
D. 3,7.10-3 mol/L
pH = -log[H+]
=> [ H + ] = 10 - p H = 10 - 2 , 44 ≈ 0 , 00363 ≈ 3 , 6 . 10 - 3 (mol/L).
Chọn đáp án C
Ta đã biết, độ pH của một dung dịch được xác định bởi \(pH = - \log \left[ {{H^ + }} \right],\) ở đó \(\left[ {{H^ + }} \right]\) là nồng độ (mol/l) của hydrogen. Tính tốc độ thay đổi của pH với nồng độ \(\left[ {{H^ + }} \right]\).
Với \(pH=-log\left[H^+\right]\),ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=\dfrac{d}{d\left[H^+\right]}\left(-log\left[H^+\right]\right)\)
Sử dụng quy tắc tính đạo hàm của hàm hợp, ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=-1.\dfrac{d}{d\left[H^+\right]}\left(log\left[H^+\right]\right)\)
Áp dụng công thức đạo hàm của hàm số logarit tổng quát, ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=-1.\dfrac{1}{\left[H^+\right]ln10}\)
Vậy tốc độ thay đổi của \(pH\) đối với nồng độ \(\left[H^+\right]\) là:
\(\dfrac{dpH}{d\left[H^+\right]}=-\dfrac{1}{\left[H^+\right]ln10}\)