Alo đề nghị viết đề một cách chính xác 

a) Ta có P = ( 4 x 2 − 1 ) ( 2 x + 1 ) − ( 2 x − 1 ) − ( 4 x 2 − 1 ) ( 2 x + 1 ) ( 2 x − 1 ) = 3 − 4 x 2  

b) Ta có  Q = 3 x ( x + 3 ) . ( x + 3 ) ( x − 3 ) − x = 9 − 3 x x + 3

ảnh lỗi r ạ

Lỗi rùi

lưu ảnh rồi gửi vào đây nhé

a)  5 x 2   –   x   +   2   =   0 ;

a = 5; b = -1; c = 2

Δ   =   b 2   -   4 a c   =   ( - 1 ) 2   -   4 . 5 . 2

= 1 - 40 = -39 < 0

Vậy phương trình trên vô nghiệm.

b) 4 x 2   –   4 x   +   1   =   0 ;

a = 4; b = -4; c = 1

Δ   =   b 2   -   4 a c   =   ( - 4 ) 2 -   4 . 4 . 1   =   16   -   16   =   0

⇒ phương trình có nghiệm kép

x = (-b)/2a = (-(-4))/2.4 = 1/2

Vậy phương trình có nghiệm duy nhất x = 1/2

c)  - 3 x 2   +   x   +   5   =   0

a = -3; b = 1; c = 5

Δ   =   b 2   -   4 a c   =   12   -   4 . ( - 3 ) . 5   =   1   +   60   =   61   >   0

⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt

x 1   =   ( 1   -   √ 61 ) / 6 ;   x 2   =   ( 1   +   √ 61 ) / 6

a) Phương trình bậc hai  4 x 2   +   4 x   +   1   =   0

Có a = 4; b’ = 2; c = 1;  Δ ’   =   ( b ’ ) 2   –   a c   =   2 2   –   4 . 1   =   0

Phương trình có nghiệm kép là:

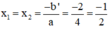
b) Phương trình  13852 x 2   –   14 x   +   1   =   0

Có a = 13852; b’ = -7; c = 1;

Δ ’   =   ( b ’ ) 2   –   a c   =   ( - 7 ) 2   –   13852 . 1   =   - 13803   <   0

Vậy phương trình vô nghiệm.

c) Phương trình bậc hai  5 x 2   –   6 x   +   1   =   0

Có: a = 5; b’ = -3; c = 1.;  Δ ’   =   ( b ’ ) 2   –   a c   =   ( - 3 ) 2   –   5 . 1   =   4   >   0

Phương trình có hai nghiệm phân biệt:

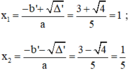
d) Phương trình bậc hai: 

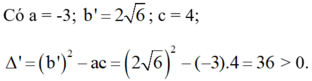
Phương trình có hai nghiệm phân biệt :

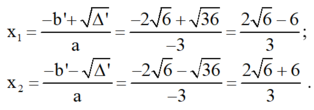
Kiến thức áp dụng

Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.

+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt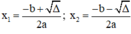 

+ Nếu Δ = 0, phương trình có nghiệm kép  ;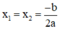

+ Nếu Δ < 0, phương trình vô nghiệm.

1.

a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)

\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)

\(\Leftrightarrow x^3+3x^2+2x-6=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)

b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)

\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)

Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)

\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)

1c/

\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)

\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)

\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn

Vậy pt có nghiệm duy nhất \(x=-1\)

2.

a. \(x^4-x^3+x^2+x^2-x+1=0\)

\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)

\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)

Vậy pt vô nghiệm

b.

\(x^4+x^3+x^2+x+1=0\)

\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)

\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)

Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)

Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn

a: \(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)

\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)

Để dư bằng 0 thì -3x+7=0

=>x=7/3

b: \(\dfrac{x^5+2x^4+3x^2+x-3}{x^2+1}\)

\(=\dfrac{x^5+x^3+2x^4+2x^2-x^3-x+x^2+1+2x-4}{x^2+1}\)

\(=x^3+2x^2-x+1+\dfrac{2x-4}{x^2+1}\)

Để đư bằng 0 thì 2x-4=0

=>x=2

Bài 1:

a) (3x - 2)(4x + 5) = 0

<=> 3x - 2 = 0 hoặc 4x + 5 = 0

<=> 3x = 2 hoặc 4x = -5

<=> x = 2/3 hoặc x = -5/4

b) (2,3x - 6,9)(0,1x + 2) = 0

<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0

<=> 2,3x = 6,9 hoặc 0,1x = -2

<=> x = 3 hoặc x = -20

c) (4x + 2)(x^2 + 1) = 0

<=> 4x + 2 = 0 hoặc x^2 + 1 # 0

<=> 4x = -2

<=> x = -2/4 = -1/2

d) (2x + 7)(x - 5)(5x + 1) = 0

<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0

<=> 2x = -7 hoặc x = 5 hoặc 5x = -1

<=> x = -7/2 hoặc x = 5 hoặc x = -1/5

bài 2:

a, (3x+2)(x^2-1)=(9x^2-4)(x+1)

(3x+2)(x-1)(x+1)=(3x-2)(3x+2)(x+1)

(3x+2)(x-1)(x+1)-(3x-2)(3x+2)(x+1)=0

(3x+2)(x+1)(1-2x)=0

b, x(x+3)(x-3)-(x-2)(x^2-2x+4)=0

x(x^2-9)-(x^3+8)=0

x^3-9x-x^3-8=0

-9x-8=0

tự tìm x nha