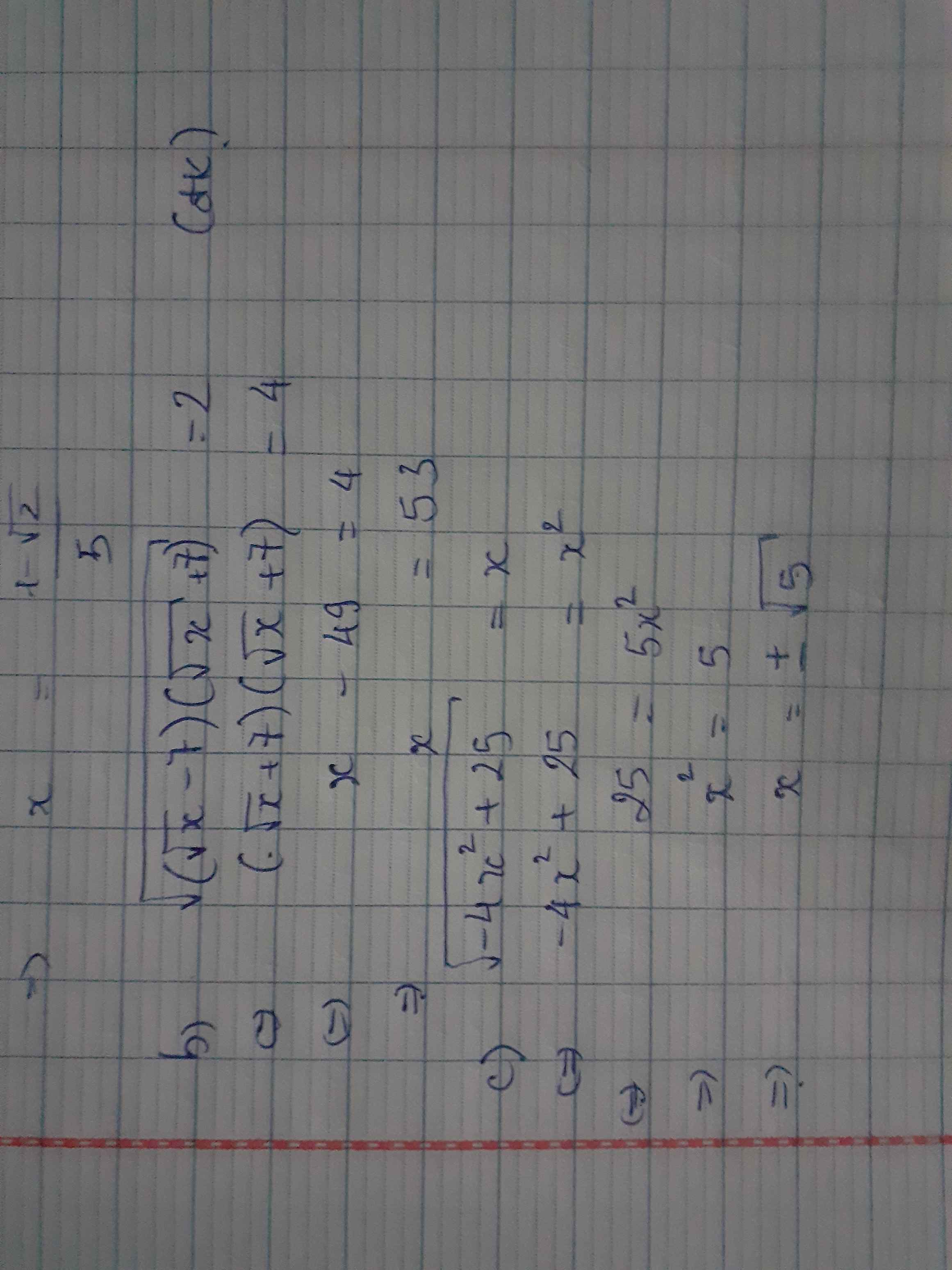Giải phương trình:\(2\left(5x+3\sqrt{x^2+x-2}\right)=27+3\sqrt{x-1}+\sqrt{x+2}\)

Những câu hỏi liên quan
giải phương trình: \(x^2+\left(3-x\right)\sqrt{2x-1}=x\left(3\sqrt{2x^2-5x+2}-\sqrt{x-2}\right)\)
bài 1,giải các phương trình saua,sqrt{5x-2}7b,sqrt{9x-27}+sqrt{25x-75}24c,x^2-5x+82sqrt{x-2}bài 2,cho Aleft{dfrac{sqrt{x}}{sqrt{x}+2}-dfrac{sqrt{x}}{sqrt{x}-2}right}divdfrac{2}{sqrt{x}+2}NÊU ĐKXĐ VÀ RÚT GỌN Abài 3,cho Bleft{dfrac{1}{sqrt{x}-1}+dfrac{sqrt{x}}{x-1}right}timesdfrac{x-sqrt{x}}{2sqrt{x}+1}NÊU ĐKXĐ VÀ RÚT GỌN Bbài4,cho Cleft(dfrac{1}{sqrt{x}-3}-dfrac{1}{sqrt{x}+3}right)timesleft(1-dfrac{3}{sqrt{x}}right)NÊU ĐKXĐ VÀ RÚT GỌN C
Đọc tiếp
bài 1,giải các phương trình sau
a,\(\sqrt{5x-2}=7\)
b,\(\sqrt{9x-27}+\sqrt{25x-75}=24\)
c,\(x^2-5x+8=2\sqrt{x-2}\)
bài 2,cho A=\(\left\{\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right\}\div\dfrac{2}{\sqrt{x}+2}\)
NÊU ĐKXĐ VÀ RÚT GỌN A
bài 3,cho B=\(\left\{\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right\}\times\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\)
NÊU ĐKXĐ VÀ RÚT GỌN B
bài4,cho C=\(\left(\dfrac{1}{\sqrt{x}-3}-\dfrac{1}{\sqrt{x}+3}\right)\times\left(1-\dfrac{3}{\sqrt{x}}\right)\)
NÊU ĐKXĐ VÀ RÚT GỌN C
Bài 1:
a. ĐKXĐ: $x\geq \frac{2}{5}$
PT $\Leftrightarrow 5x-2=7^2=49$
$\Leftrightarrow 5x=51$
$\Leftrightarrow x=\frac{51}{5}=10,2$
b. ĐKXĐ: $x\geq 3$
PT $\Leftrightarrow \sqrt{9(x-3)}+\sqrt{25(x-3)}=24$
$\Leftrightarrow 3\sqrt{x-3}+5\sqrt{x-3}=24$
$\Leftrightarrow 8\sqrt{x-3}=24$
$\Leftrightarrow \sqrt{x-3}=3$
$\Leftrightarrow x-3=9$
$\Leftrightarrow x=12$ (tm)
Đúng 2
Bình luận (0)
Bài 1:
c. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow x^2-5x+6-2(\sqrt{x-2}-1)=0$
$\Leftrightarrow (x-2)(x-3)-2.\frac{x-3}{\sqrt{x-2}+1}=0$
$\Leftrightarrow (x-3)[(x-2)-\frac{2}{\sqrt{x-2}+1}]=0$
$x-3=0$ hoặc $x-2=\frac{2}{\sqrt{x-2}+1}$
Nếu $x-3=0$
$\Leftrightarrow x=3$ (tm)
Nếu $x-2=\frac{2}{\sqrt{x-2}+1}$
$\Leftrightarrow a^2=\frac{2}{a+1}$ (đặt $\sqrt{x-2}=a$)
$\Leftrightarrow a^3+a^2-2=0$
$\Leftrightarrow a^2(a-1)+2a(a-1)+2(a-1)=0$
$\Leftrightarrow (a-1)(a^2+2a+2)=0$
Hiển nhiên $a^2+2a+2=(a+1)^2+1>0$ với mọi $a$ nên $a-1=0$
$\Leftrightarrow a=1\Leftrightarrow \sqrt{x-2}=1\Leftrightarrow x=3$ (tm)
Vậy pt có nghiệm duy nhất $x=3$.
Đúng 2
Bình luận (0)
Bài 2:
ĐKXĐ: $x\geq 0; x\neq 4$
\(A=\frac{\sqrt{x}(\sqrt{x}-2)-\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}+2)\sqrt{x}-2)}.\frac{\sqrt{x}+2}{2}\\ =\frac{-4\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}+2}{2}\\ =\frac{-2\sqrt{x}}{\sqrt{x}-2}=\frac{2\sqrt{x}}{2-\sqrt{x}}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình: \(2.\left(x-\sqrt{2x^2+5x-3}\right)=1+x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow2x-2\sqrt{2x^2+5x-3}=1+x\sqrt{2x-1}-2x\sqrt{x+3}\\ \Leftrightarrow\left(2x-2\right)-\left(2\sqrt{2x^2+5x-3}-4\right)=\left(x\sqrt{2x-1}-x\right)-\left(2x\sqrt{x+3}-4x\right)-3x+3\\ \Leftrightarrow2\left(x-1\right)-\dfrac{2\left(2x^2+5x-7\right)}{\sqrt{2x^2+5x-3}+4}=\dfrac{x\left(2x-2\right)}{\sqrt{2x-1}+1}-\dfrac{2x\left(x-1\right)}{\sqrt{x+3}+4x}-3\left(x-1\right)\\ \Leftrightarrow2\left(x-1\right)-\dfrac{2\left(x-1\right)\left(2x+7\right)}{\sqrt{2x^2+5x-3}+4}-\dfrac{2x\left(x-1\right)}{\sqrt{2x-1}+1}+\dfrac{2x\left(x-1\right)}{\sqrt{x+3}+4x}+3\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left[2-\dfrac{2\left(2x+7\right)}{\sqrt{2x^2+5x-3}+4}-\dfrac{2x}{\sqrt{2x-1}+2}+\dfrac{2x}{\sqrt{x+3}+4x}+3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\2-\dfrac{2\left(2x+7\right)}{\sqrt{2x^2+5x-3}+4}-\dfrac{2x}{\sqrt{2x-1}+2}+\dfrac{2x}{\sqrt{x+3}+4x}+3=0\left(1\right)\end{matrix}\right.\)
Với \(x\ge\dfrac{1}{2}\Leftrightarrow-\dfrac{2\left(2x+7\right)}{\sqrt{2x^2+5x-3}+4}>-\dfrac{2\cdot8}{4}=-4\)
\(-\dfrac{2x}{\sqrt{2x-1}+2}>-\dfrac{1}{2};\dfrac{2x}{\sqrt{x+3}+4x}>0\)
Do đó \(\left(1\right)>2-4-\dfrac{1}{2}+3=\dfrac{1}{2}>0\) nên (1) vô nghiệm
Vậy PT có nghiệm duy nhất \(x=1\)
Đúng 1
Bình luận (0)
Giải phương trình sau:
1, \(\sqrt{5x+3}\) = \(\sqrt{3-\sqrt{2}}\)
2, \(\sqrt{\left(\sqrt{x}-7\right)\left(\sqrt{x}+7\right)}\) = 2
3,\(\sqrt{-4x^2+25}=x\)
1. ĐKXĐ: $x\geq \frac{-3}{5}$
PT $\Leftrightarrow 5x+3=3-\sqrt{2}$
$\Leftrightarrow x=\frac{-\sqrt{2}}{5}$
Đúng 1
Bình luận (0)
2. ĐKXĐ: $x\geq \sqrt{7}$
PT $\Leftrightarrow (\sqrt{x}-7)(\sqrt{x}+7)=4$
$\Leftrightarrow x-49=4$
$\Leftrightarrow x=53$ (thỏa mãn)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình sau
1. \(5x^2-16x+7+\left(x+1\right)\sqrt{x^2+3x-1}=0\)
2. \(3\left(\sqrt{2x^2+1}-1\right)=x\left(1+3x+8\sqrt{2x^2+1}\right)\)
\(\left(\frac{2x-1}{2-x}+2\sqrt{2-x}\right)^3=27\left(2x-1\right)\)
Giải phương trình nghiệm nguyên sau:
\(3x^3-13x^2+30x-4=\sqrt{\left(6x+2\right)\left(3x-4\right)^3}\)
Giải phương trình:
a) \(5x^2-10x=4\left(x-1\right)\sqrt{x^2-2x+2}\)
b) \(\sqrt{2x^2+22x+29}-x-2=2\sqrt{2x+3}\)
c) \(x^3-7x^2+9x+12=\left(x-3\right)\left(x-2+5\sqrt{x-3}\right)\left(\sqrt{x-3}-1\right)\)
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
giải phương trình :
a, \(\sqrt{x+1}+x+3=\sqrt{1-x}+3\sqrt{1-x^2}\)
b,\(\left(2x-3\right)\sqrt{3+x}+2x\sqrt{3-x}=6x-8+\sqrt{9-x^2}\)
c, \(2x^2-5x+22=5\sqrt{x^3-11x +20}\)
d, \(x^3-3x^2+2\sqrt{\left(x+2\right)^3}=6x\)
a) Giải phương trình trên tập số thực:
\(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
b) Giải hệ phương trình sau:
\(\left\{{}\begin{matrix}x^2+2x\sqrt{xy}=y^2\sqrt{y}\\\left(4x^3+y^3+3x^2\sqrt{x}\right)\left(15\sqrt{x}+y\right)=3\sqrt{x}\left(y\sqrt{y}+x\sqrt{y}+4x\sqrt{x}\right)^2\end{matrix}\right.\) ; với \(x,y\inℝ\)
a) \(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow-7x^2-9x+4+x^3+3x^2+4x+2=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow-\left(7x^2+9x-4\right)+\left(x+1\right)^3+x+1=\sqrt[3]{7x^2+9x-4}\) (*)
Đặt \(\sqrt[3]{7x^2+9x-4}=a;x+1=b\)
Khi đó (*) \(\Leftrightarrow-a^3+b^3+b=a\)
\(\Leftrightarrow\left(b-a\right).\left(b^2+ab+a^2+1\right)=0\)
\(\Leftrightarrow b=a\)
Hay \(x+1=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow\left(x+1\right)^3=7x^2+9x-4\)
\(\Leftrightarrow x^3-4x^2-6x+5=0\)
\(\Leftrightarrow x^3-4x^2-5x-x+5=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-1\pm\sqrt{5}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)