vẽ đồ thị vận tốc thời gian của hàm số v=2t

Những câu hỏi liên quan
một xe chuyển động thẳng biến đổi đều với phương trình
x=5+10t -1/2t ( mũ hai )
a) xá định quãng đường vật đi được sau 6 s
b) viết công thức tính vận tốc tại thời điểm t
c) vẽ đồ thị vận tốc - thời gian
giúp em với ạ ( em cần gấp :<< )
<Mình nghĩ là bạn đã thiếu đơn vị.Nên mình lấy đơn vị m/s>
Ta có :\(x=5+10t-\dfrac{1}{2}t^2\left(m,s\right)\Rightarrow v_0=10\left(\dfrac{m}{s}\right);x_0=5\left(m\right);a=-1\left(\dfrac{m}{s^2}\right)\)
a, Quãng đường vật đi được sau 6s
\(s=10\cdot6-\dfrac{1}{2}\cdot6^2=42\left(m\right)\)
b,Vận tốc tại thời điểm t là
\(v=10-t\)
c<bạn tự vẽ nha, Dùng phương trình ở câu b để làm y chang cái lúc mình vẽ đồ thị hàm số ở lớp 9 nhớ trục tung là v(m/s) và trục hoành là t(s)
Đúng 1
Bình luận (0)
Một vật chuyển động thẳng biến đổi đều có đồ thị vận tốc v theo thời gian t như hình vẽ. Phương trình vận tốc của vật là: A. v 15 – t(m/s) B. v t + 15(m/s) C. v 10 – 5t(m/s) D. v 10 – 15t(m/s)
Đọc tiếp
Một vật chuyển động thẳng biến đổi đều có đồ thị vận tốc v theo thời gian t như hình vẽ. Phương trình vận tốc của vật là:
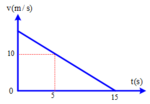
A. v = 15 – t(m/s)
B. v = t + 15(m/s)
C. v = 10 – 5t(m/s)
D. v = 10 – 15t(m/s)
Một chiếc xe máy chuyển động thẳng đều trên quỹ đạo AB100km theo chiều A đến B với vận tốc 50km/h. Khi xe Đi qua A vào lúc 6h sáng. Chọn gốc toạ độ tại A chiều dương từ A đến B, gốc thời gian lúc 6h.
a, Lập phương trình vận tốc thời gian. Vẽ đồ thị vận tốc thời gian đó
b, Lập phương trình toạ độ thời gian và ve đồ thị
c, Tính đường Đi của vật lúc 10h,12h
d, Vẽ đồ thị đường Đi theo thời gian.
Đọc tiếp
Một chiếc xe máy chuyển động thẳng đều trên quỹ đạo AB=100km theo chiều A đến B với vận tốc 50km/h. Khi xe Đi qua A vào lúc 6h sáng. Chọn gốc toạ độ tại A chiều dương từ A đến B, gốc thời gian lúc 6h.
a, Lập phương trình vận tốc thời gian. Vẽ đồ thị vận tốc thời gian đó
b, Lập phương trình toạ độ thời gian và ve đồ thị
c, Tính đường Đi của vật lúc 10h,12h
d, Vẽ đồ thị đường Đi theo thời gian.
a) Phương trình vận tốc thời gian
\(v=\frac{s}{t}\Rightarrow50=\frac{100}{t}\)
b) phương trình tọa độ thời gian:
\(x=x_0+vt=50t\)
Lúc 10, thời gian xe đi:
\(t=10h-6h=4h\)
Quãng đường đi được của xe máy
\(x=50.4=200\left(km\right)\)
Lúc 12h, thời gian t là:
\(t=12-6=6h\)
=> \(x=50.6=300\left(km\right)\)
Đúng 0
Bình luận (0)
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t 0,2 s, độ dốc bằng 0 một lần nữa. Từ t 0,2 s đến t 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ -...
Đọc tiếp
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).
Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …
Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
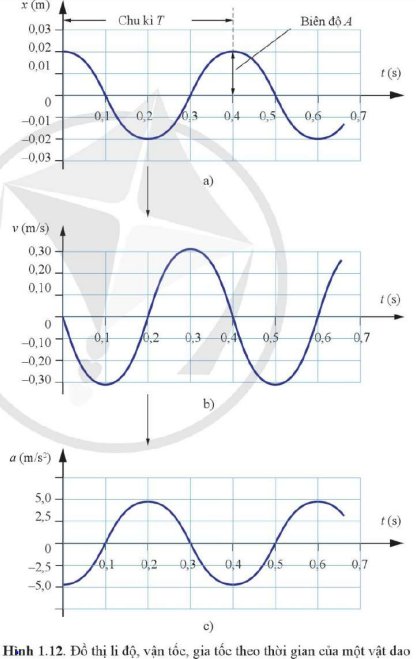
Dựa vào các đồ thị ở Hình `1.12` ta có:
- Các thời điểm gia tốc của xe bằng `0` là `t={0,1 ; 0,3 ; 0,5} (s)`
- Các thời điểm gia tốc của xe cực đại là `t={0 ; 0,2 ; 0,4 ; 0,6} (s)`
Cách làm: dựa vào đồ thị ở hình `c`, ta chiếu các thời điểm ứng với trục `t` sang trục `a`.
Đúng 1
Bình luận (0)
Một người đi bộ với vận tốc đều 5 km/ha
a) Hãy biểu diễn quãng đường y(km) người đó đi được thời gian x(giờ)
b) Vẽ đồ thị hàm số đó
c) Từ đồ thị hàm số hãy cho biết trong 2 giờ người đó đi được bao nhiêu km?
Một người đi bộ vs vận tốc đều 5km/h
a) Hãy biểu diễn quãng đường y(km) người đó đi đc trong thời gian x(h)
b) Vẽ đồ thị hàm số đó
c) Từ đồ thị hàm số hãy cho biết trong 2 h người đó đi đc bao nhiêu km?
Đồ thị vận tốc theo thời gian của chuyển động thẳng như hình vẽ. Chuyển động thẳng nhanh dần đều là đoạn v (m/s) A. MN B. NO C. OP D. PQ
Đọc tiếp
Đồ thị vận tốc theo thời gian của chuyển động thẳng như hình vẽ. Chuyển động thẳng nhanh dần đều là đoạn v (m/s)
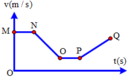
A. MN
B. NO
C. OP
D. PQ
Một người đi bộ với vận tốc đều 5km/h.
a.Hãy biểu diễn quãng đường y(km) người đó đi đc thời gian x (giờ)?
b. Vẽ đồ thị hàm số đó.
Một vật chuyển động trong 5 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của parabol có đỉnh I(2;8) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là những đoạn thẳng (như hình vẽ). Tính quãng đường s mà vật di chuyển được trong 5 giờ đó. A. 25 km. B. 41 km. C. 33 km. D. 26 km.
Đọc tiếp
Một vật chuyển động trong 5 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của parabol có đỉnh I(2;8) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là những đoạn thẳng (như hình vẽ). Tính quãng đường s mà vật di chuyển được trong 5 giờ đó.
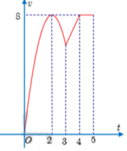
A. 25 km.
B. 41 km.
C. 33 km.
D. 26 km.



















