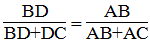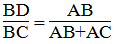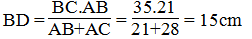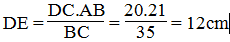Cho tam giác ABC vuông tại A. Đường phân giác trong của góc B cắt AC tại D. Biết BD=4,25cm, CD= 3,95cm. Tính AD ?

Những câu hỏi liên quan
cho tam giác ABC vuông tại A, có đường phân giác của góc B cắt AC tại D, biết BD=7cm, CD=15cm. Tính AD
Bài 1: Cho tam giác ABC, có AB = 6cm, BC = 10cm. Các đường phân giác trong và ngoài của góc B cắt AC lần lượt tại D và E. Tính BD và BE.
Bài 2: Cho tam giác ABC vuông tại A, đường phân giác trong AD, đường cao AH, CD = 68cm, BD = 51cm. Tính BH
Bài 4. Cho tam giác ABC vuông tại A, biết AB = 21cm, AC = 28cm, đường phân giác AD. Đường thẳng qua D và song song với AB cắt AC tại E. a) Tính độ dài BD, CD, ED. b) Đường thẳng vuông góc với AD tại A cắt BE kéo dài tại F. Tính độ dài BF.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=212+282=1225BC2=AB2+AC2=212+282=1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠∠(BAC) nên:
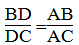
Suy ra:
Hay
Suy ra:
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: 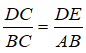
Suy ra:
Đúng 2
Bình luận (0)
a: BC=35(cm)
Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó: BD=15(cm); CD=20(cm)
Xét ΔABC có ED//AB
nên ED/AB=CD/CB
=>ED/21=20/35=4/7
=>ED=12(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A: AB = 6cm, AC = 8cm. Kẻ phân giác trong
BD của góc ABC (D thuộc AC).
a) Tính AD, CD b) Vẽ đường cao AH. Tính AH, HC
c) Tia phân giác góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh
BIM là góc vuông
a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)
Cho tam giác ABC vuông tại A. Đường phân giác góc B cắt AC tại D, cho AB= 6cm, BC= 10cm
a) Tính AC, AD, CD
b) Từ D kẻ đường thẳng vuông góc với AC cắt BC tại K. Qua K kẻ đường thẳng vuông góc với BD tại E và cắt AB, AC lần lượt tại F,H. Chứng minh tam giác ABC đồng dạng tam giác DHK
C) Chứng minh BFDK: hình thoi
Cho tam giác ABC vuông tại A có AH là đường cao, BD là phân giác góc B với D thuộc AC. AH cắt BD tại I. Tính tỉ số AI/AB và AD/AB Cho tam giác ABC vuông tại A có AH là đường cao,BD là phân giác góc B với D thuộc AC. AH cắt BD tại I.
a, tính tỉ số AI/AB và AD/AB
B,Cm: tam giác AID cân tại A C, cm: IH/BH = DC/BC
a: Xét ΔABH có BI là phân giác
nên \(\dfrac{AI}{AB}=\dfrac{IH}{BH}\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
Đề bài này chưa đủ dữ kiện để tính cụ thể AI/AB; AD/AB nha bạn
b: ΔBAD vuông tại A
=>\(\widehat{ABD}+\widehat{ADB}=90^0\)
=>\(\widehat{ADI}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\left(1\right)\)
ΔBIH vuông tại H
=>\(\widehat{HBI}+\widehat{BIH}=90^0\)
=>\(\widehat{BIH}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ADI}=\widehat{BIH}\)
mà \(\widehat{AID}=\widehat{BIH}\)(hai góc đối đỉnh)
nên \(\widehat{ADI}=\widehat{AID}\)
=>ΔAID cân tại A
=>AD=AI(3)
Xét ΔABH có BI là phân giác
nên \(\dfrac{IH}{BH}=\dfrac{AI}{AB}\left(4\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DC}{BC}=\dfrac{DA}{AB}\left(5\right)\)
Từ (3),(4),(5) suy ra \(\dfrac{IH}{BH}=\dfrac{DC}{BC}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có đường phân giác là AD. Biết AB = 21cm, AC = 28cm. Đường thẳng qua D song song với AB cắt ac tại E.
a) Tính CD, BD, ED
b) Đường thẳng vuông góc với AD tại A cắt BC kéo dài tại E. Tính BF
Câu b là kéo dài tại F ạ,tại mk ghi nhầm:)))
Đúng 0
Bình luận (0)
#hoa học trò# chưa bn ơi,bạn biết làm bài này ko,bạn giúp mình với
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A: AB = 6cm, AC = 8cm. Kẻ phân giác trong
BD của góc ABC (D thuộc AC).
a) Tính AD, CD b) Vẽ đường cao AH. Tính AH, HC
c) Tia phân giác góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh
\(\widehat{BIM}\)là góc vuông
Cho tam giác ABC vuông tại A. Phân giác góc B cắt AC tại D. BD=3,87 và CD=3,56.Tính AD