\(n_{Zn}=\dfrac{3,25}{65}=0,05\left(mol\right)\)
pthh : \(Zn+2HCl->ZnCl_2+H_2\)
           0,05                                  0,05 
\(n_{CuO}=\dfrac{6}{80}=0,075\left(mol\right)\)
pthh : \(H_2+CuO-t^o->Cu+H_2O\)
 LTL : 
\(\dfrac{0,05}{1}< \dfrac{0,075}{1}\)
=> CuO dư 
theo pthh : nCu = nH2 =0,05 (mol)
=> \(m_{Cu}=0,05.64=3,2\left(g\right)\)
theo pthh : \(n_{CuO\left(p\text{ư}\right)}=n_{H_2}=0,05\left(mol\right)\)
=> \(n_{CuO\left(d\right)}=0,075-0,05=0,025\left(mol\right)\)
=>\(m_{CuO}=0,025.80=2\left(g\right)\)

\(n_{Al}=\dfrac{2,7}{27}=0,1\left(mol\right)\)

PTHH: 2Al + 3H₂SO₄ ---> Al₂(SO₄)₃ + 3H₂

          0,1          0,15             0,05           0,15

PbO + H₂ --to--> Pb + H₂O

0,15    0,15

\(\rightarrow\left\{{}\begin{matrix}a=0,15.98=14,7\left(g\right)\\V=0,15.22,4=3,36\left(l\right)\\m_{PbO}=0,15.233=34,95\left(g\right)\end{matrix}\right.\)

\(n_{Al}=\dfrac{2,7}{27}=0,1\left(mol\right)\)
pthh : \(4Al+6H_2SO_4->2Al_2\left(SO_4\right)_3+3H_2\)
           0,1      0,6                                      0,3 
=> \(V=V_{H_2}=0,3.22,4=6,72\) (L) 
=> a = \(m_{H_2SO_4}=0,6.98=58,8\left(g\right)\)
pthh : \(PbO+H_2->H_2O+Pb\)
          0,3       0,3 
=> \(m_{PbO}=0,3.217=65,1\left(g\right)\)
 

Bài 10: A

Bài 11:

Áp dụng hệ thức về cạnh và góc trong tam giác vào tam giác vuông, ta được:
AC = AB.tan\(^{50^0}\) = 21.tan\(^{50^0}\) \(\approx\) 25

BC = \(\dfrac{AB}{\sin C}\)= \(\dfrac{21}{sin40^0}\)\(\approx\)33

BD = \(\dfrac{AB}{\cos25^0}\)=\(\dfrac{21}{\cos25^0}\)\(\approx\)23

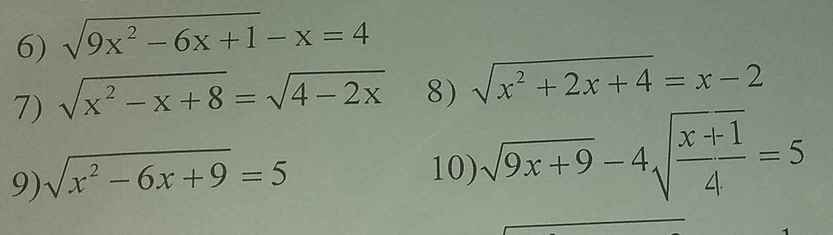
7)Đk \(x\le2\)

Pt \(\Leftrightarrow x^2-x+8=4-2x\)

\(\Leftrightarrow x^2+x+4=0\)

\(\Delta=-15< 0\) => vô nghiệm

Vậy pt vô nghiệm

10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)

\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)

\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)

\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)

Vậy \(S=\left\{24\right\}\)

1D 2B 3C 4A 5A 6C 7A 8A 9B 10A 11C 12D 13D 14D 15A 16D 17A 18C 19C 20D 21D 22C 23C 24A 25B 26C 27D 28B 29C

1 D

2 B

3 C

4 A

5 A

Câu 10:

$\sin ^2x=0\Leftrightarrow \sin x=0$

$\Rightarrow x=k\pi$ với $k$ nguyên.

Trong các khoảng đã cho chỉ có khoảng ở đáp án A chứa $k\pi$ với $k$ nguyên.

Câu 11:

PT\(\Leftrightarrow 2\sin x\cos x-\sin x-2+4\cos x=0\)

\(\Leftrightarrow 2\cos x(\sin x+2)-(\sin x+2)=0\)

\(\Leftrightarrow (2\cos x-1)(\sin x+2)=0\)

Vì $\sin x\geq -1$ nên $\sin x+2\geq 1>0$

$\Rightarrow 2\cos x-1=0$

$\Leftrightarrow \cos x=\frac{1}{2}=\cos \frac{\pi}{3}$

$\Rightarrow x=\frac{\pi}{3}+2k\pi$ hoặc $x=-\frac{\pi}{3} +2k\pi$ với $k$ nguyên.

Đáp án B.

10: B

33: B

34: D

35: D

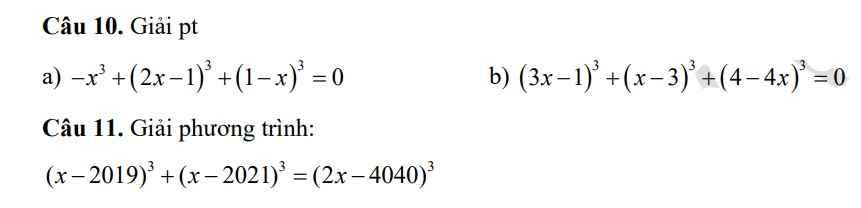
Câu 10:

a: \(\Leftrightarrow-x^3+8x^3-12x^2+6x-1+1-3x+3x^2-x^3=0\)

\(\Leftrightarrow6x^3-9x^2+3x=0\)

\(\Leftrightarrow3x\left(2x^2-3x+1\right)=0\)

\(\Leftrightarrow x\left(2x-1\right)\left(x-1\right)=0\)

hay \(x\in\left\{0;\dfrac{1}{2};1\right\}\)

b: Đặt 3x-1=a; x-3=b

Theo đề, ta có: \(a^3+b^3-\left(a+b\right)^3=0\)

\(\Leftrightarrow a^3+b^3-a^3-b^3-3a^2b-3ab^2=0\)

\(\Leftrightarrow3ab\left(a+b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x-3=0\\4-4x=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{1}{3};3;1\right\}\)

\(S=\int\limits^2_{-3}\left|f\left(x\right)\right|dx=-\int\limits^1_{-3}f\left(x\right)dx+\int\limits^2_1f\left(x\right)dx\)

(Phần nằm dưới trục hoành thêm dấu - đằng trước, phần nằm trên trục hoành giữ nguyên dấu)