Cho tam giác ABCvuông tại A. Gọi M,N,P lần lượt là trung điểm của BC,CA,AB. Xác định tâm O đường tròn đi qua ba điểm M,N,P. Đường tròn này còn đi qua điểm nào khác?

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là trung điểm của AC và BC. Xác định tâm đường tròn đi qua ba điểm H, M, N và tính bán kính đường tròn nếu AH = 3cm và BA = 5cm.
Áp dụng định lý pagota vào tam giác ABC vuông tại A
Đúng 0
Bình luận (0)
Bạn trình bày rõ hơn một chút được không
Đúng 0
Bình luận (0)
Cho tam giác ABC không cân tại A. Đường tròn (O) thay đổi đi qua B và C theo thứ tự cắt AB, AC lần lượt tại M và N. Gọi P là giao điểm của BN và CM. Q là điểm chính giữa cung BC không chứa M,N của (O). K là tâm đường tròn nội tiếp tam giác PBC. CMR: KQ luôn đi qua 1 điểm cố định
Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm CM và DN
a, Tính số đo góc CEN
b, Chứng minh A, D, E, M cùng thuộc một đường tròn
c, Xác định tâm của đường tròn đi qua ba điểm B, D, E

a, Chứng minh ∆CMB = ∆DNC => N C E ^ = C D N ^
Từ đó chứng minh được C E N ^ = 90 0
b, Ta có A,D,E,M cùng thuộc được tròn đường kính DM
c, Gọi I là trung điểm của CD, chứng minh AI song song với MC
=> ∆ADE cân tại A
=> B,E,D cùng thuộc (A;AB)
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc đường tròn (O), với C khác A và B, biết CA CB. Lấy điểm M thuộc đoạn OB, với M khác O và B. Đường thẳng đi qua điểm M vuông góc với AB cắt hai đường thẳng AC và BC lần lượt tại hai điểm D và H.1) Chứng minh bốn điểm A, C, H, M cùng thuộc một đường tròn và xác định tâm của đường tròn này.2) Chứng minh: MA.MB MD.MH3) Gọi E là giao điểm của đường thẳng BD với đường tròn (O), E khác B. Chứng minh ba điểm A, H, E thẳng hàng.4) Trên tia đối của tia...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc đường tròn (O), với C khác A và B, biết CA < CB. Lấy điểm M thuộc đoạn OB, với M khác O và B. Đường thẳng đi qua điểm M vuông góc với AB cắt hai đường thẳng AC và BC lần lượt tại hai điểm D và H.
1) Chứng minh bốn điểm A, C, H, M cùng thuộc một đường tròn và xác định tâm của đường tròn này.
2) Chứng minh: MA.MB = MD.MH
3) Gọi E là giao điểm của đường thẳng BD với đường tròn (O), E khác B. Chứng minh ba điểm A, H, E thẳng hàng.
4) Trên tia đối của tia BA lấy điểm N sao cho MN = AB, Gọi P và Q tương ứng là hình chiếu vuông góc của điểm M trên BD và N trên AD.
Chứng minh bốn điểm D, Q, H, P cùng thuộc một đường tròn.
mk bt nhưng mk ko bt
Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của BC, CA, AB và O là tâm đường tròn ngoại tiếp tam giác ABC.
a. CM: A, F, O, E thuộc 1 đường tròn
b. Các đường trong (AEF), (BFD), (CDE) bằng nhau và cùng đi qua 1 điểm. Xác định điểm chung đó
giải nhanh mình tick cho nha
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
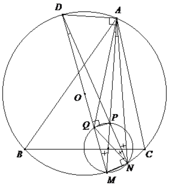
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Điểm I di động trên cạnh BC. Gọi D,E lần lượt là hình chiếu của I trên AB và AC. Lấy M đối xứng với A qua D, N đối xứng với A qua E. Chứng minh:
a) I là tâm đường tròn đi qua 3 điểm A,M,N
b) Đường tròn (I) nói trên đi qua 1 điểm cố định khác A

Huy làm có gì sai mọi người góp ý nha :3
a
Ta có 2 đường trung trực của các đoạn thẳng AM,AN cắt nhau tại I nên I là tâm đường tròn ngoại tiếp tam giác AMN
b
Hạ đường cao AK. Gọi L đối xứng với A qua K. Suy ra L cố định.Ta sẽ chứng minh tứ giác AMLN nội tiếp. Thật vậy !
Ta dễ có được đường tròn tâm I ngoại tiếp tam giác ALN
Ta có:\(\widehat{AIN}=2\widehat{ALN};\widehat{AIN}=2\widehat{AMN}\Rightarrow\widehat{ALN}=\widehat{AMN}\) nên tứ giác AMLN nội tiếp khi đó đường tròn I luôn đi qua điểm L cố định
Hình tui đã vẽ trong TKHĐ nhé :))
Mình làm ra vở cho bạn rồi nhé. Chữ mình hơi xấu, mong bạn thông cảm.
Xin lỗi bạn nhiều lắm, vừa nãy mình gửi thiếu ảnh.



Xem thêm câu trả lời
Cho nửa đường tròn tâm (O) có đường kính AB.lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung AB ( M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM,BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai Na) chứng minh: ACMD nội tiếpb) chứng minh: CA.CB CH.CDc) Chứng minh; ba điểm A,N,D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DNd) khi M...
Đọc tiếp
Cho nửa đường tròn tâm (O) có đường kính AB.lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung AB ( M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM,BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai N
a) chứng minh: ACMD nội tiếp
b) chứng minh: CA.CB= CH.CD
c) Chứng minh; ba điểm A,N,D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DN
d) khi M di chuyển trên cung KB. chứng minh đường thẳng MN luôn đi qua 1 điểm cố định.
Cho nửa đường tròn tâm (O) có đường kính AB.lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung AB ( M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM,BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai Na) chứng minh: ACMD nội tiếpb) chứng minh: CA.CB CH.CDc) Chứng minh; ba điểm A,N,D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DNd) khi M...
Đọc tiếp
Cho nửa đường tròn tâm (O) có đường kính AB.lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung AB ( M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM,BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai N
a) chứng minh: ACMD nội tiếp
b) chứng minh: CA.CB= CH.CD
c) Chứng minh; ba điểm A,N,D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DN
d) khi M di chuyển trên cung KB. chứng minh đường thẳng MN luôn đi qua 1 điểm cố định.
















