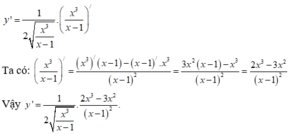A= -căn bặc 2 của x+1 +5

Những câu hỏi liên quan
Bài 1 Cho x=căn bặc ba của ( 16-8can5) + căn bặc ba của (16+8can5). Tính f(x)=(x^3+12x-31)^2013
Bài 2 cho f(x)=(x^4+x^3+39x-103)^2016. Tính f(a) biét a= căn bặc ba của( 7+5can2) +căn bặc ba của (7-5can2)
Ai giỏi toán giúp mik
căn bặc x+2 + căn bặc 3-x
ĐKXĐ: x+2>=0 và 3-x>=0
=>-2<=x<=3
Đúng 0
Bình luận (0)
cho các x,y,z thỏa mãn x/2 = x/3 = x/4 và x+ 2y - 3z = -20. Tính A= căn bặc 2 của x+6y + z+ 1
Cho A= căn bặc 2 của x cộng với 1 trên căn bậc 2 của x trừ một tìm gt nhỏ nhất của A đề vt toàn chữ vì ko vt đc công thức thông cảm!
\(A=\sqrt{x}+\dfrac{1}{\sqrt{x-1}}\)
Đề có phải vậy?
Đúng 0
Bình luận (0)
tìm x biết
căn bặc 2 của x=2
\(\sqrt{x}=2\)
\(x=2^2\)
\(\Rightarrow x=4\)
Đúng 0
Bình luận (0)
Bài 1: xét dấu tam thức bậc hai
1.f(x)= -1/2 x^2
2.f(x)=x^2-2x-1
3.v=-x^2-4x+1
4.v=x^2+x+1
5.v=-x^2+4x+6
6.y= căn bặc hai 2x^2
7.y=((1-căn bậc hai 2)x^2-2x-1
8.v=2(x+3)^2-5
9.v= trừ căn bậc hai 2^2+4x
cho X^2-2mx+4=0 có 2 nghiệm x1,x1 ko giải PT tính Căn bậc 3 x1 + căn bặc 3 x2
Tính đạo hàm của hàm số
y
x
3
x
-
1
(Áp dụng căn bặc hai của u đạo hàm). A. B. C. D.
Đọc tiếp
Tính đạo hàm của hàm số y = x 3 x - 1 (Áp dụng căn bặc hai của u đạo hàm).
A. 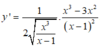
B. 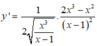
C. 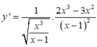
D. 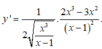
cho mặt cầu (S): x^2 + y^2 + z^2 -2x -2y -2z =0 và điểm A(2;2;2). Điểm B thay đổi trên mặt cầu. Diện tích của tam giác OAB có giá trị lớn nhất là?
A. 1 (đvdt)
B. 2 (đvdt)
C. căn bặc hai của 3 (đvdt)
D, 3 (đvdt)
Lời giải:
Ta có:
\((S): x^2+y^2+z^2-2x-2y-2z=0\)
\(\Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2=3\)
Do đó mặt cầu \((S)\) có tâm \(O=(1,1,1)\) và \(R=\sqrt{3}\)
Khi đó, dễ dàng nhận thấy \(A\in (S)\)
Ta có \(S_{OAB}=\frac{OA.OB.\sin \angle AOB}{2}\leq \frac{OA.OB.1}{2}=\frac{3}{2}\) vì \(\sin AOB\leq 1\)
Dấu bằng xảy ra khi \(\angle AOB=90^0\)
Đúng 0
Bình luận (1)