Chứng minh rằng: \(\overrightarrow{AN}+\overrightarrow{NM}=\overrightarrow{0}\)

Những câu hỏi liên quan
Cho cho tứ giác lồi $A B C D$. Gọi $E, F$ lần lượt là trung điểm của $A B, C D$ và $G$ là trung điểm $E F$. Chứng minh rằng:
a) $\overrightarrow{A C}+\overrightarrow{B D}=\overrightarrow{A D}+\overrightarrow{B C}=2 \overrightarrow{E F}$.
b) $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G D}=\overrightarrow{0}$
a ) Ta có: FC + FD = EB + EA (=0)
=> AC - AF + AD - AF = EA + AB + EA
=> AC + BA + AD = EA + AF + EA +AF
=> AC + BD = EF + EF
=> AC + BD = 2EF ( 1 )
Ta lại có : AB = AC + CB ( quy tắc 3 điểm ) ; AB = AD + DB ( quy tắc 3 điểm )
=> AC + CB = AD + DB
=> AC - DB = AD - CB
=> AC + BD = AD + BC ( 2 )
Từ (1),(2) => AC + BD = AD + BC = 2EF
b ) Ta có: GE + GF + GE + GF = 0
=> GA + AE + GC + CF + GB + BE + GD + DF = 0
=> GA + GC + GD + GB = - AE - CF - BE - DF
=> GA + GB + GC + GD = EA + EB + FC + FD
mà E , F lần lượt là trung điểm AB , DC => EA + EB = 0 ; FD + DC = 0
Vậy => GA + GB + GC + GD = 0 + 0 = 0
Đúng 0
Bình luận (0)
Cho tam giác $A B C$. Hai điểm $M, N$ được xác định bởi hệ thức $\overrightarrow{B C}+\overrightarrow{M A}=\overrightarrow{0}$, $\overrightarrow{A B}-\overrightarrow{N A}-3 \overrightarrow{A C}=\overrightarrow{0}$. Chứng minh rằng $M N / / A C$.
Cho lục giác đều $A B C D E F$ tâm $O$. Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}+\overrightarrow{O F}=\overrightarrow{0}$.
Xem thêm câu trả lời
Cho ngũ giác đều $A B C D E$ tâm $O$.
a) Chứng minh rằng: hai vectơ $\overrightarrow{O A}+\overrightarrow{O B}$ và $\overrightarrow{O C}+\overrightarrow{O E}$ đều cùng phương với $\overrightarrow{O D}$.
b) Chứng minh hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{E C}$ cùng phương.
c) Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}=\overrightarrow{0}$.
Xem thêm câu trả lời
Cho hình bình hành ABCD , 2 điểm E ; F thỏa mãn 2 \(\overrightarrow{CE}+\overrightarrow{EB}=\overrightarrow{0},3\overrightarrow{DF}+\overrightarrow{BD}=\overrightarrow{0}\)
1. Chứng minh A ; E ; F thẳng hàng
2. Tìm M sao cho \(2\overrightarrow{AM}-3\overrightarrow{AF}=\overrightarrow{0}\)
Cho tứ giác $A B C D$. Gọi hai điểm $M$ và $N$ theo thứ tự là trung điêm của các đoạn $A D, B C$.
a) Chứng minh rằng $\overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C})=\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{D B})$.
b) Gọi $I$ là trung điểm của $M N$. Chứng minh rằng: $\overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}+\overrightarrow{I D}=\overrightarrow{0}$.
mik cg ko bik nha a hihi
mình không biết mình lớp 3
Xem thêm câu trả lời
Cho tam giác ABC, Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. Chứng minh rằng :
a, \(\overrightarrow{\text{Ạ}N}=\overrightarrow{AM}+\overrightarrow{AP}\)
b, \(\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{0}\)
\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}=\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{AC}}{2}=\overrightarrow{AM}+\overrightarrow{AP}\)
\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\)
\(\overrightarrow{BP}=\frac{\overrightarrow{BA}+\overrightarrow{BC}}{2}\)
\(\overrightarrow{CM}=\frac{\overrightarrow{CB}+\overrightarrow{CA}}{2}\)
\(\Rightarrow\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
đường tròn nội tiếp (I) của tam giác ABC theo thứ tự tiếp xúc với các cạnh BC,CA,AB tại D,E,F. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
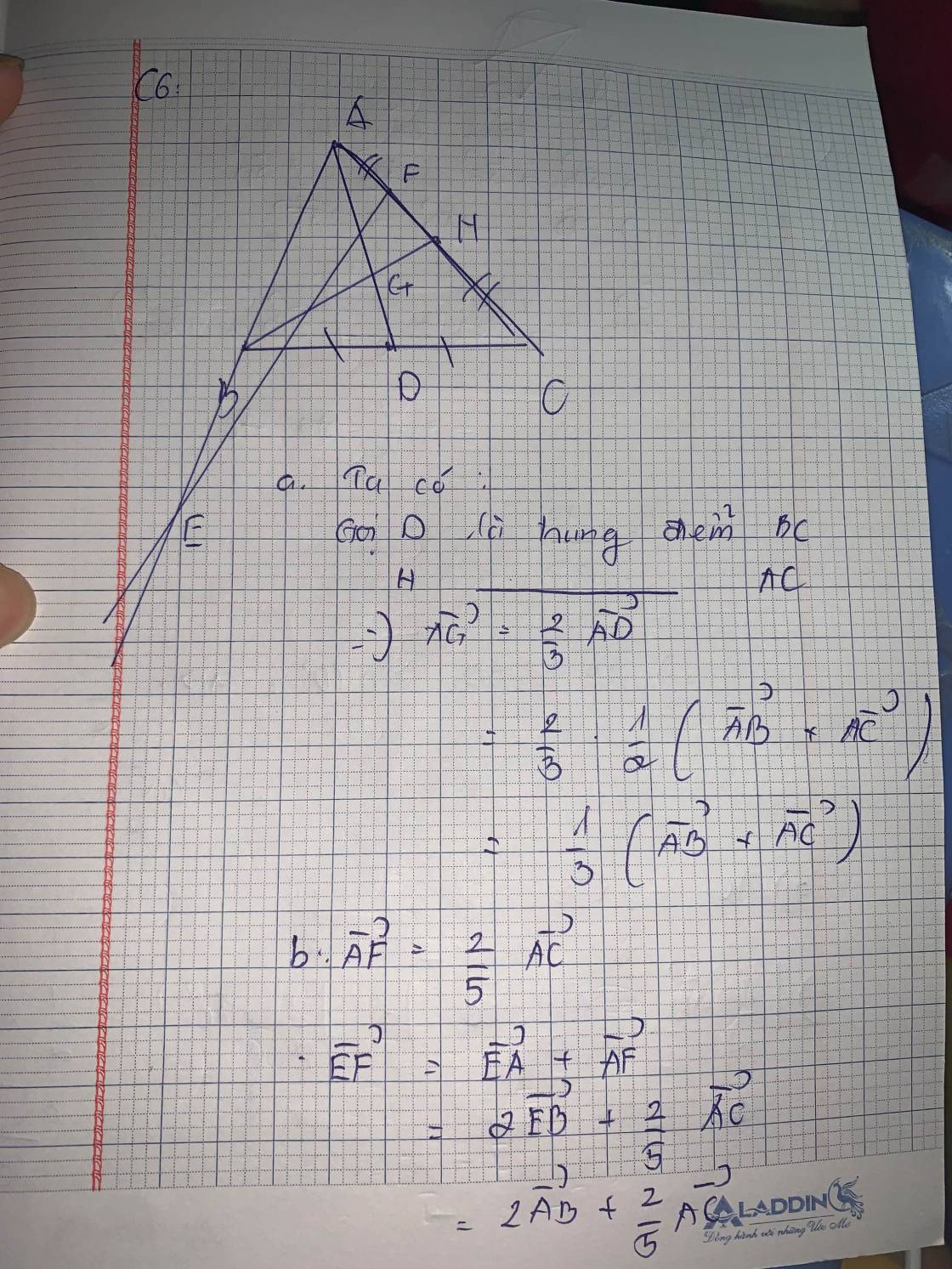
Cho tam giác $A B C$ có $G$ là trọng tâm.
a) Hāy phân tích véctơ $\overrightarrow{A G}$ theo hai vectơ $\overrightarrow{A B}, \overrightarrow{A C}$.
b) Gọi $E, F$ là hai điểm xác định bởi các điều kiện: $\overrightarrow{E A}=2 \overrightarrow{E B}, 3 \overrightarrow{F A}+2 \overrightarrow{F C}=\overrightarrow{0}$. Hāy phân tích $\overrightarrow{E F}$ theo hai vecto $\overrightarrow{A B}, \overrightarrow{A C}$.
Xem thêm câu trả lời







 đúng ko v ???????
đúng ko v ???????