Hai đường thẳng (d): y=2x-3 và (d`): y=-x+2m-1 cắt nhau tại 1 điểm trên trục Oy. Khi đó giá trị của m thuộc khoảng nào ?
A. (4;8)
B. (-1;1)
C.(1;3)
D. (-3;0)
Định m để:
a) Hai đường thẳng (d): y=2x-1 +2m và (d'): y=-x-2m cắt nhau tại 1 điểm có hoành độ dương
b) Hai đường thẳng (D1): mx+y=2m và (D2): (2m+1)x+my=2m^2 + m -1 cắt nhau tại 1 điểm trên trục tung. Tìm điểm đó
a.Tìm các giá trị của m để đường thẳng y = 2x - m2 - m đi qua điểm A(1 ; 0)
b.Tìm m để hai đường thẳng sau cắt nhau tại một điểm thuộc trục hoành:
(d): y = 2x + 4 và (d'): y = x + m - 2
a.
Để đường thẳng đi qua A
\(\Rightarrow2.1-m^2-m=0\Leftrightarrow m^2+m-2=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
b.
Hoành độ giao điểm của (d) với trục hoành:
\(2x+4=0\Rightarrow x=-2\Rightarrow\) hai đường thẳng cắt nhau tại (-2;0)
(d') đi qua (-2;0) nên:
\(-2+m-2=0\Rightarrow m=4\)
a, Giải hệ phương trình: x + 1 y - 1 = x y - 1 x - 3 y - 3 = x y - 3
b, Trên mặt phẳng tọa độ Oxy, cho prabol (P): y = x 2 và đường thẳng d: y = 2 x + m 2 - 2 m . Tìm các giá trị của m để d cắt (P) cắt tại hai điểm phân biệt nằm về hai phía của trục tung Oy
a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 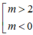
Kết luận 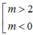
Trong mặt phẳng Oxy, cho 2 đường thẳng (d): y= (m-3)x + n + 5 và (d'): y=-2x + 1. Tìm giá trị của m,n để hai đường thẳng (d) và (d') cắt nhau tại một điểm trên trục tung
Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
Tìm giá trị của m để đường thẳng (d1): y = 2x - m + 1 và (d2): y = ( 2m + 1 )x + 2m - 5 cắt nhau tại một điểm thuộc trục tung
Để (d1) và (d2) cắt nhau tại một điểm thuộc trục tung thì \(\left\{{}\begin{matrix}2\ne2m+1\\-m+1=2m-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m\ne1\\-m-2m=-5-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\-3m=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\m=2\end{matrix}\right.\Leftrightarrow m=2\)
Vậy: m=2
Cắt nhau tại 1 điểm trên trục tung <=>
\(\left\{{}\begin{matrix}a-khác-a'\\b=b'\end{matrix}\right.< =>\left\{{}\begin{matrix}2-khác-2m+1\\-m+1=-5\end{matrix}\right.< =>\left\{{}\begin{matrix}m-khác-\dfrac{1}{2}\\m=6\end{matrix}\right.\)
Đường thẳng d: y = (m − 3)x − 2m + 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là:
A. 1
B. 0
C. 3
D. 2
cho đường thẳng (d) có phương trình y = (2m - 1)x + m + 1 và đường thẳng (d') có phương trình y = x+ 3
a, tính giá trị của m để đường thẳng (d) cắt đường thẳng (d') tại một điểm trên trục tung
b, tìm m để khoản cách từ gốc tọa độ O đến dường thẳng (d) đạt giá trị lớn nhất và giá trị lớn nhất đó bằng nhau
Cho parabol (P): y=x và đường thẳng (d): y =2mx−m’ +2m+1 a) Vẽ (P). b) Với giá trị nào của m thì (P) và (d) cắt nhau tại hai điểm phân biệt cùng nằm bên phải trục tung.