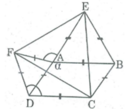
Vì ∠ (BAD) +  ∠ (BAE) +  ∠ (EAF) +  ∠ (FAD) = 360 0

⇒  ∠ (EAF) =  360 0  – ( ∠ (BAD) +  ∠ (BAE) +  ∠ (FAD) )

Mà  ∠ (BAD) = α 2  (gt)

∠ (BAE) =  60 0  (ΔBAE đều)

∠ (FAD) =  60 0  (ΔFAD đều)

Nên  ∠ (EAF) =  360 0  – ( α 2  +  60 0  +  60 0 ) =  240 0  –  α

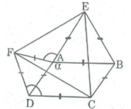
Ta có:

∠ (BAD) + ∠ ∠ (ADC) = 180 0  (hai góc trong cùng phía bù nhau)

⇒  ∠ (ADC) =  180 0  -  ∠ (BAD) =  180 0  – α

∠ (CDF) =  ∠ (ADC) +  ∠ (ADF) =  180 0  - α 2 + 60 0 = 240 0 - α

Suy ra:  ∠ (CDF) =  ∠ (EAF)

Xét  ∆ AEF và ∆ DCF: AF = DF ( vì  ∆ ADF đều)

AE = DC (vì cùng bằng AB)

∠ (CDF) =  ∠ (EAF) (chứng minh trên)

Do đó:  ∆ AEF =  ∆ DCF (c.g.c) ⇒ EF = CF (1)

∠ (CBE) =  ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α

Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)

∠ (CBE) =  ∠ (CDF) = 240 0 - α

BC = DF (vì cùng bằng AD)

Do đó  ∆ BCE =  ∆ DFC (c.g.c) ⇒ CE = CF (2)

Từ (1) và (2) suy ra: EF = CF = CE

Vậy  ∆  ECF đều.

a) Vì ABCD là hình bình hành 

=> AB = CD ( tính chất) 

AD//BC 

AB//CD 

AD = BC ( tính chất) 

BAD = BCD ( tính chất) 

Vì E là trung điểm AD 

=> AE = ED 

Vì F là trung điểm BC 

=> BF = FC 

Mà AD = BC 

AE = ED = BF = FC

Xét ∆ABE và ∆FCD ta có : 

AB = CD 

AE = BF (cmt)

BAD = FCD ( cmt)

=> ∆ABE = ∆FCD (c.g.c)

b) Vì E\(\in\)AD 

F \(\in\)BC 

Mà AD//BC 

=> ED//BF 

Mà ED = BF ( cmt)

=> EBFD là hình bình hành ( dấu hiệu nhận biết) 

c) Vì ABCD là hình bình hành 

=> AC và BD là 2 đường chéo cắt nhau tại trung điểm mỗi đường 

Hay AC và BD cắt nhau tại trung điểm BD (1)

Vì EBCD là hình bình hành 

=> BD và FE là 2 đường chéo cắt nhau tại trung điểm mỗi đường 

Hay FE và BD cắt nhau tại trung điểm BD (2)

Từ (1) và (2) => AC , BD , FE cắt nhau tại trung điểm BD 

=> AC,BD ,FE đồng quy

Hình bình hành lớp 8? | Yahoo Hỏi & Đáp

Tính góc EAF 

EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1) 

b) Chứng minh rằng tam giác CEF là tam giác đều 

ABC^ = ADC^ = 180* - a 

=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2) 

CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3) 

AF = DF = AD = BC (4) 

CD = AB = BE = AE (5) 

(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c) 

=> CF = CE = EF => CEF là tam giác đều

a, tính gócEAF

AEF^= 360- (DAF^+BAD^+BAE^)= 360 -(60+a+60)= 240-a (1)

b, chứng minh rằng tam giác CEF là tam giác đều

ABC^= ADC^=180 -a

=>CDF^=ADC^+ADF^=180-a+60=240-a (2)

CBE^=ABC^+ABE^=180-a+60=240-a (3)

AF=DF=AD=BC (4)

CD=AB=AE=BE (5)

Từ (1) (2) (3) (4) (5)=> tam giácCDF= tam giác EBC= tam giác EAF (c.g.c)

=>CF= CE= EF=> tam giác CEF ĐỀU

đó là câu b

nụ hôn trên giường