cho đoạn AB và hai điểm E ,K thuộc đoạn AB sao cho AE =BK . chứng minh rằng AB và EK có cùng trung điểm

Những câu hỏi liên quan
1.cho đoạn AB và hai điểm E ,K thuộc đoạn AB sao cho AE =BK . chứng mình rằng AB và EK có cùng trung điểm
1.cho đoạn AB và hai điểm E ,K thuộc đoạn AB sao cho AE BK . chứng mình rằng AB và EK có cùng trung điểm2. cho bốn đường thẳng thì số giao điểm của bốn đường thẳng này có thể bằng bao nhiêu ?3. từ n điểm mà không có ba điểm nào thẳng hàng người ta lập nên các đường thẳng từ hai điểm trong đó . HỎI n bằng bao nhiêu nếu số đường thẳng là 105 đường
Đọc tiếp
1.cho đoạn AB và hai điểm E ,K thuộc đoạn AB sao cho AE =BK . chứng mình rằng AB và EK có cùng trung điểm
2. cho bốn đường thẳng thì số giao điểm của bốn đường thẳng này có thể bằng bao nhiêu ?
3. từ n điểm mà không có ba điểm nào thẳng hàng người ta lập nên các đường thẳng từ hai điểm trong đó . HỎI n bằng bao nhiêu nếu số đường thẳng là 105 đường
1) A---------E--------------------M--------------------K----------B
Gọi M là trung điểm của AB => AM =BM = AB/2
Vì AE = BK
+ Nếu AE < AM như hình vé => AM -AE = MB - BK => EM = MK => M là trung điểm của EK
+ Nếu AE > AM tự vẽ hình
=> AE - AM = BK - MB => EM = E=MK => M là trung điểm của EK
Vậy AB;EK có chung trung điểm là M
2) 4 đường thẳng ( phân biệt hay ko ?)
3) n(n-1):2 =105 => n(n-1) =210 =15.14
=> n = 15
Đúng 0
Bình luận (0)
Cho tam giác ABC có AC > AB, M là trung điểm của BC. Lấy điểm D thuộc đoạn MB, điểm E thuộc đoạn MC sao cho BD = CE. Vẽ điểm K sao cho M là trung điểm của AK. Chứng minh rằng: a) AD + DK < AB + BK b) AD + AE < AB + AC
1. Cho tam giác ABC có góc A < 90o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD, AE sao cho: AD _|_ AB, AD = AB và AE _|_ AC, AE = AC. Chứng minh rằng: DC = BE và DC _|_ BE
2. Cho tam giác ABC có góc A < 90o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD, AE sao cho: AD _|_AB, AD = AB và AE _|_ AC, AE = AC. Từ B kẻ BK _|_ CD tại K. Chứng minh rằng 3 điểm E,K,B thẳng hàng
Cho tam giác abc có ba góc nhọn vẽ đoạn thẳng AD vuông góc với AB và AD AB (D và C nằm về hai phía với đối với AB). Vẽ đoạn thẳng AE vuông góc AC, AE AC ( E và B nằm về 2 phía đối với AC). Kẻ AH vuông góc với BC tại H. Kẻ DI và EK cùng vuông góc với đường thẳng AH (I và K thuộc đường thẳng AH). Chứng minh rằng : a) Tam giác ABH Tam giác DAI. b) DI EKc) Gọi M là giao điểm của DE và KI. Chứng minh rằng M là trung điểm của DE và KI.
Đọc tiếp
Cho tam giác abc có ba góc nhọn vẽ đoạn thẳng AD vuông góc với AB và AD = AB (D và C nằm về hai phía với đối với AB). Vẽ đoạn thẳng AE vuông góc AC, AE = AC ( E và B nằm về 2 phía đối với AC). Kẻ AH vuông góc với BC tại H. Kẻ DI và EK cùng vuông góc với đường thẳng AH (I và K thuộc đường thẳng AH).
Chứng minh rằng :
a) Tam giác ABH = Tam giác DAI.
b) DI = EK
c) Gọi M là giao điểm của DE và KI. Chứng minh rằng M là trung điểm của DE và KI.
cho mình thời gian đến tối nay nha lát nữa mình bận mình hứa mình sẽ giải
Đúng 0
Bình luận (0)
Mình làm tắt nha
a, Ta có: góc ADI = góc HAB (cùng phụ vs DAI)
=> tam giác ABH = tam giác DAI (ch+gn)
b,Tam giác ABH = tam giác DAI (phần a)
=>DI=AH (1)
Ta có: góc KEA = góc HAC (cùng phụ vs KAE)
=>tam giác KEA = tam giác HAC (ch+gn)
=> EK=AH (2)
Từ 1 và 2 => DI=EK
c, Ta có: góc DMI = góc KME (đối đỉnh)
=> góc MDI = góc MEK
=> Tam giác MDI = tam giác MEK (cgv+gn)
=>MI=MK và MD=ME
=> M là trung điểm của DE và KI
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho đoạn thẳng AB = 2a. Lấy các điểm E và F nằm giữa A và B sao cho AE = BF. Chứng tỏ rằng hai đoạn thẳng AB và EF cùng có chung một đường trung trực
Trường hợp :
Gọi M là trung điểm của AB. Khi đó MA = MB = a.
Điểm E nằm giữa hai điểm A và M, điểm F nằm giữa hai điểm B và M.
Do đó ME = MA - AE = a - AE; MF = MB - BF = a - BF.
Vì AE = BF nên ME = MF. Vậy M là trung điểm chung của hai đoạn thẳng AB và EF. Qua M vẽ thì xy là đường trung trực chung của AB và EF.
Trường hợp : Chứng minh tương tự
Đúng 0
Bình luận (0)
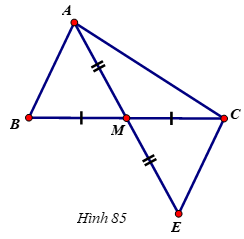
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA lấy điểm E sao cho ME MA. Chứng minh rằng AB//CEa, Chứng minh Tam giác AMBEMCb, Chứng minh AB//CE và ABCEc, Lấy điểm H thuộc cạnh AB và điểm K thuộc cạnh CE sao cho AHEK. Chứng minh ba điểm H, M, K thẳng hàngGiúp mình với ạ
Đọc tiếp
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA lấy điểm E sao cho ME = MA. Chứng minh rằng AB//CE
a, Chứng minh Tam giác AMB=EMC
b, Chứng minh AB//CE và AB=CE
c, Lấy điểm H thuộc cạnh AB và điểm K thuộc cạnh CE sao cho AH=EK. Chứng minh ba điểm H, M, K thẳng hàng
Giúp mình với ạ
a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>AB=CE
Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔHAM và ΔKEM có
HA=KE
\(\widehat{HAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔHAM=ΔKEM
=>\(\widehat{AMH}=\widehat{EMK}\)
mà \(\widehat{AMH}+\widehat{HME}=180^0\)(hai góc kề bù)
nên \(\widehat{EMK}+\widehat{HME}=180^0\)
=>H,M,E thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn.Vẽ đoạn thẳng AD vuông góc với AB,AD=AB( D và C nằm về hai phía đối với AB).Vẽ đoạn thẳng AE vuông góc với AC,AE=AC(E và B nằm về hai phía đối với AC ).Kẻ AH vuông góc với đường thẳng BC tại H.Kẻ DI và EK cùng vuông góc với đường thẳng AH(I và K thuộc đường thẳng AH) .CM rằng: DI=EK, DE và KI cắt nhau tại trung điểm của mỗi đường
1) Cho đoạn thẳng AB 8cm. Gọi M là trung điểm của AB. Điểm K thuộc tia AB sao cho AK 2cm. Chứng minh rằng K là trung điểm của AM.2) Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng d vuông góc với AB. Gọi C là 1 điểm thuộc d : a) Chứng minh tam giác AMC tam giác BMCb) Lấy H thuộc đoạn thẳng AM, điểm K thuộc đoạn thẳng BM sao cho AH BK. Chứng minh rằng CH CK
Đọc tiếp
1) Cho đoạn thẳng AB = 8cm. Gọi M là trung điểm của AB. Điểm K thuộc tia AB sao cho AK = 2cm. Chứng minh rằng K là trung điểm của AM.
2) Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng d vuông góc với AB. Gọi C là 1 điểm thuộc d :
a) Chứng minh tam giác AMC = tam giác BMC
b) Lấy H thuộc đoạn thẳng AM, điểm K thuộc đoạn thẳng BM sao cho AH = BK. Chứng minh rằng CH = CK
1 , vì M là trung điểm của AB nên
AM=BM=8:2=4(cm)
ta có:BD+MD=BM
\(\Rightarrow\)3+MD=4
\(\Rightarrow\)MD=1(cm)
ta có:AC+MC=AM
\(\Rightarrow\)3+CM=4
\(\Rightarrow\)CM=1(cm)
mà CD=CM+MD=1+1=2(cm)
b,vì CM+MD=CD:2
\(\Rightarrow\)suy ra M là trung điểmCD
Đúng 0
Bình luận (0)