Mọi người ơi , giúp em 2 bài này nha! Theo hằng đẳng thức ạ! ( dấu "^" là mũ , " - " là trừ , dấu "." là nhân còn mấy cái sô với chữ em viết liền nhau là nó nhân với nhau nha mọi người )
Bài 1
a) cho x^2 = y^2 + z^2 . Chứng minh rằng: ( 5x - 3y + 4z ) . ( 5x - 3y - 4z ) = ( 3x - 5y )^2 ( tất cả mũ 2 nha mn)
b ) cho 10x^2 ( x mũ 2 ) = 10y^2 ( y mũ 2 ) + z^2 . Chứng minh rằng : ( 7x - 3y + 2z ) . ( 7x - 3y - 2z ) = ( 3x - 2y )^2 ( tất cả mũ 2 nha)
c ) Cho x+y = a , x^2 + y^2 =b ; x^3 + y^3 = c. Chứng minh rằng : a^2 - 3ab ( 3 nhân a nhân b nha ) + 2c = 0
Bài 2 : Tìm x:
a) x.(x+4) . ( 4-x ) + ( x-5) . (x^2 + 5x + 25 ) = 3
b) ( x+1)^3 - ( x - 1)^3 - 6.( x-1)^2 = -10 ( âm 10 nha)







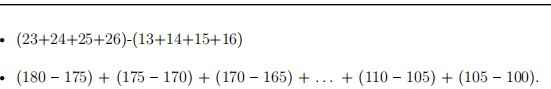 bài b dấu chấm là trừ 5 cho đến khi nào tới 105 .
bài b dấu chấm là trừ 5 cho đến khi nào tới 105 .
















