Cho tam giác ABC đường cao AH. Gọi D,E lần lượt là trung điểm của AB và AC. Vẽ DI và EK cùng vuông góc với BC. Chứng minh rằng:
a) DI = EK
b) IK =1/2 BC
Những câu hỏi liên quan
Cho tam giác ABC có đường cao AH. Gọi D, E lần lượt là trung điểm của AB , AC. Vẽ DI và EK cùng vuông góc với BC
chứng minh rằng
a, DI = EK b. IK = 1/2 BC
a. Xét tam giác ABH có DI//AH(cùng vuông góc với BC) và D là TĐ AB nên DI là đường TBinh của tam giác ABH => DI=1/2 AH
Làm Tương tự ta có: EK là đường TB tam giác AHC => EK=1/2 AH
=> DI=EK
b. Theo Chứng minh phần a:
DI là đường TB tam giác ABH => I là TĐ BH
EK là đường TB tam giác AHC => K là TĐ HC
=> IK= IH+HK= 1/2 BH + 1/2HC =1/2BC
Đúng 1
Bình luận (0)
Bài 4: Cho tam giác ABC. Vẽ đường cao AH. Gọi D, E theo thứ tự là trung điểm của các cạnh AB và AC. Vẽ DI và EK cùng vuông góc với BC. Chứng minh rằng :DI = EK. Gợi ý : - Học sinh tự vẽ hình minh họa. - dựa vào đường trung bình chứng minh DI = 1/2 AH và EK = 1/2AH.
cho Tam giác ABC , vẽ đường cao Ag . Gọi D,E lần lượt là trung điểm của AB,AC
ve DI vuông góc AB , Ek vuông góc với BC
C/m : a) DI = Ek
b)IK = BC
BT: Cho tam giác ABC vuông tại A, đường cao AH, gọi D,E lần lượt là chân các đường vuông góc kẻ từ H đến AB và AC a) Chứng minh AH=DE b) Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh DI song song với EK
Xem chi tiết
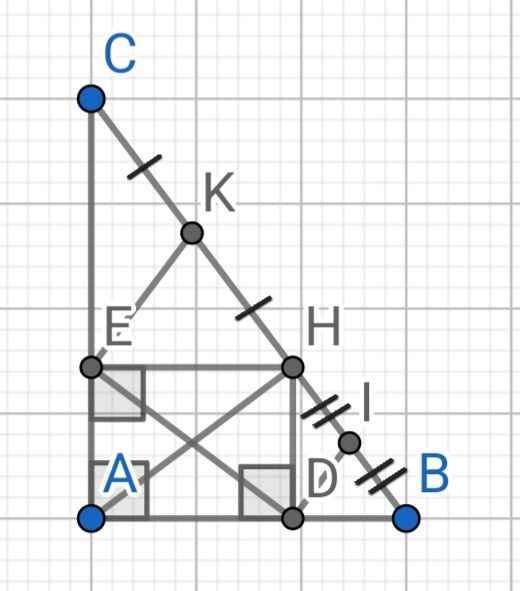a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn. Ở phía ngoài tam giác, vẽ tam giác vuông cân: Tam giác ABD và tam giác ACE. Kẻ AH vuông góc BC tại H. Từ D và E kẻ DI, EK lần lượt vuông góc với AH
A,Chứng minh DI=AH
B,Chứng minh A,H, trung điểm của DE thẳng hàng
C, Gọi M là trung điểm của BC. Chứng minh: AM vuông góc DE
Cho tam giác abc có ba góc nhọn vẽ đoạn thẳng AD vuông góc với AB và AD AB (D và C nằm về hai phía với đối với AB). Vẽ đoạn thẳng AE vuông góc AC, AE AC ( E và B nằm về 2 phía đối với AC). Kẻ AH vuông góc với BC tại H. Kẻ DI và EK cùng vuông góc với đường thẳng AH (I và K thuộc đường thẳng AH). Chứng minh rằng : a) Tam giác ABH Tam giác DAI. b) DI EKc) Gọi M là giao điểm của DE và KI. Chứng minh rằng M là trung điểm của DE và KI.
Đọc tiếp
Cho tam giác abc có ba góc nhọn vẽ đoạn thẳng AD vuông góc với AB và AD = AB (D và C nằm về hai phía với đối với AB). Vẽ đoạn thẳng AE vuông góc AC, AE = AC ( E và B nằm về 2 phía đối với AC). Kẻ AH vuông góc với BC tại H. Kẻ DI và EK cùng vuông góc với đường thẳng AH (I và K thuộc đường thẳng AH).
Chứng minh rằng :
a) Tam giác ABH = Tam giác DAI.
b) DI = EK
c) Gọi M là giao điểm của DE và KI. Chứng minh rằng M là trung điểm của DE và KI.
cho mình thời gian đến tối nay nha lát nữa mình bận mình hứa mình sẽ giải
Đúng 0
Bình luận (0)
Mình làm tắt nha
a, Ta có: góc ADI = góc HAB (cùng phụ vs DAI)
=> tam giác ABH = tam giác DAI (ch+gn)
b,Tam giác ABH = tam giác DAI (phần a)
=>DI=AH (1)
Ta có: góc KEA = góc HAC (cùng phụ vs KAE)
=>tam giác KEA = tam giác HAC (ch+gn)
=> EK=AH (2)
Từ 1 và 2 => DI=EK
c, Ta có: góc DMI = góc KME (đối đỉnh)
=> góc MDI = góc MEK
=> Tam giác MDI = tam giác MEK (cgv+gn)
=>MI=MK và MD=ME
=> M là trung điểm của DE và KI
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông ở A có AH là đường cao . Gọi D và E lần lượt là hình chiếu của H xuống AB và AC . Gọi I là trung điểm của HB , K là trung điểm của HC . Chứng minh :
a, DI // EK
b, Gọi F là trung điểm IK . Chứng minh tam giác DEF cân .
Bài 4: Cho tam giác ABC. Gọi D là trung điểm của AB, E là trung điểm của BC. Biết AC = 8cm. DE Tính
Bài 5: Cho tam giác ABC vuông tại A (AB<AC), đường cao AH Tử H vẽ HE và HF lần lượt vuông góc với AB và AC (E = AB Fe AD.
a) Chứng minh AH = EF b) Trên tia FC xác định điểm K sao cho FK = AF. Chứng minh tử giác EHKF là hinh binh hành
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC.
a) Gọi I là trung điểm HD, K là trung điểm HC. Chứng minh DI // EK
b) Gọi M là trung điểm BC, chứng minh AM // EK và AM vuông góc với DE
Bạn tham khảo bài làm ở đường link phía dưới nhé:
Câu hỏi của Nguyễn Desmond - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)